概要
树:是n个结点的有限集。当n=0时称为空树。在任意一个非空树中:
- 有且仅有一个特定称为根的结点
- 当n>1时,其余结点可分为m(m>0)个互不相交的有限集T1、T2、…、Tm,其中每个集合本身又是一棵树,并且称为根的子树。
度:结点拥有的子树数称为结点的度,树的度取树内各结点的度的最大值。
- 度为0的结点称为叶结点或终端结点
- 度不为0的结点称为分支结点或非终端结点,除根节点外,分支结点也称为内部结点
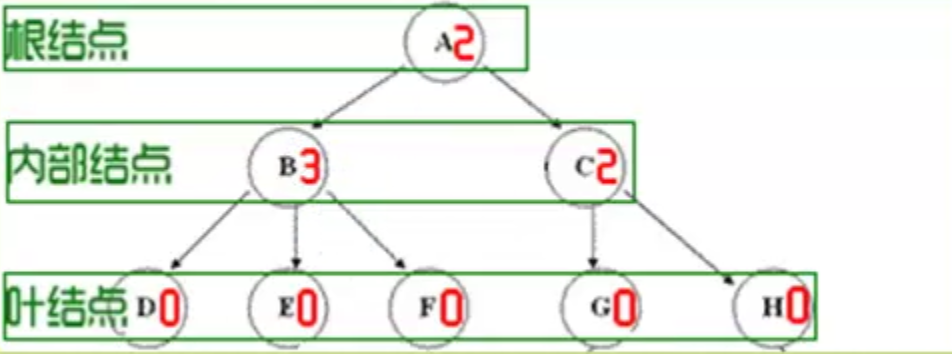
树中结点的最大层次称为树的深度或高度。
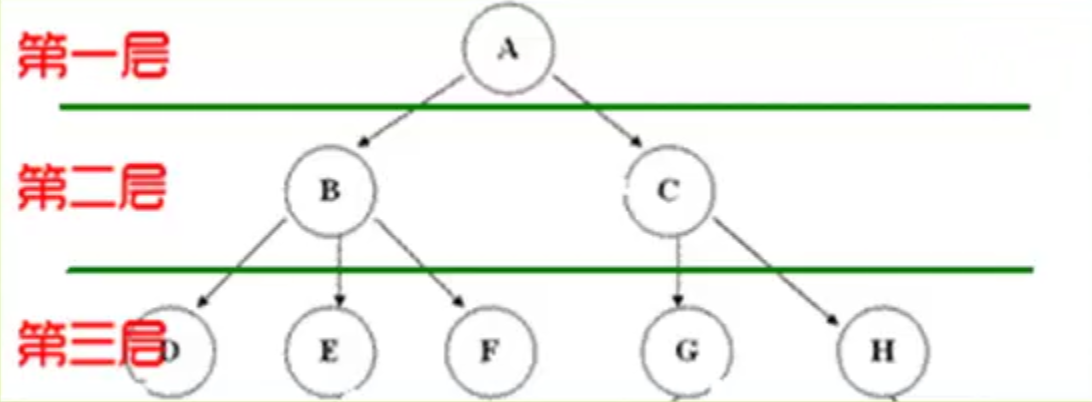
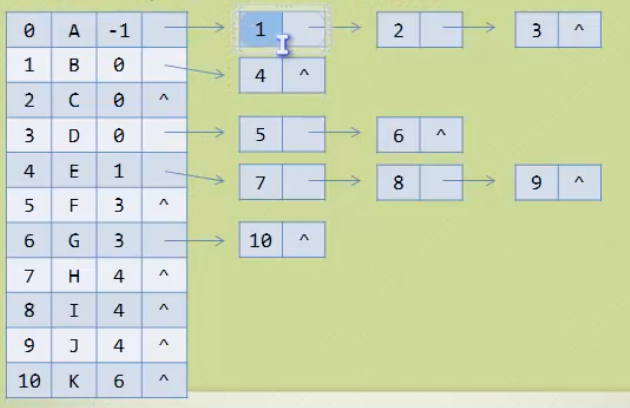
双亲表示法、孩子表示法、孩子双亲表示法、孩子兄弟表示法
二叉树
二叉树是n个结点的有限集,该集合或者为空集,或者由一个根节点和两棵互不相交的、分别称为根节点的左子树和右子树的二叉树组成。
二叉树的五种基本形态:
- 空二叉树
- 只有根节点的二叉树
- 根节点只有左子树
- 根节点只有右子树
- 根节点有左子树和右子树
特殊二叉树:
- 斜树:要么只有左子树,要么只有右子树。
- 满二叉树:所有分支结点都有左子树和右子树,并且所有叶子都在同一层上。
- 完全二叉树:编号为i的结点与同样深度的满二叉树中编号为i的结点位置完全相同。
二叉树的性质:
- 在二叉树的第i层,至多有2^(i-1)个结点。
- 深度为k的二叉树,至多有2^k - 1个结点。
- 终端结点数为n0,度为2的结点数为n2,则n0=n2+1。(假设度为1的结点数为n1,则总结点数n=n0+n1+n2,且连接数为n-1,也为n1+2*n2,推到可得)
- 具有n个结点的完全二叉树的深度为⎣log2n⎦ + 1。
- 一棵有n个结点的完全二叉树的结点按层序编号,对任一结点i(1<=i<=n)有以下性质:
- i = 1,则结点是二叉树的根
- i > 1,其双亲结点为⎣i/2⎦
- 2i > n,则结点无左孩子,否则其左孩子是结点2i
- 2i + 1 > n,则结点无右孩子,否则其右孩子是结点2i + 1
二叉树的存储结构:

二叉树的遍历:
- 前序遍历:若二叉树为空,则空操作返回,否则先访问根节点,然后前序遍历左子树,再前序遍历右子树
- 中序遍历:若二叉树为空,则空操作返回,否则中序遍历左子树,然后访问根节点,再中序遍历右子树
- 后序遍历:若二叉树为空,则空操作返回,否则从左到右先叶子后结点的方式遍历访问左右子树,最后访问根节点
- 层序遍历:若二叉树为空,则空操作返回,否则从树的第一层开始向下,按从左到右的顺序对结点逐个访问
创建二叉树用前序遍历的方式是最简单的
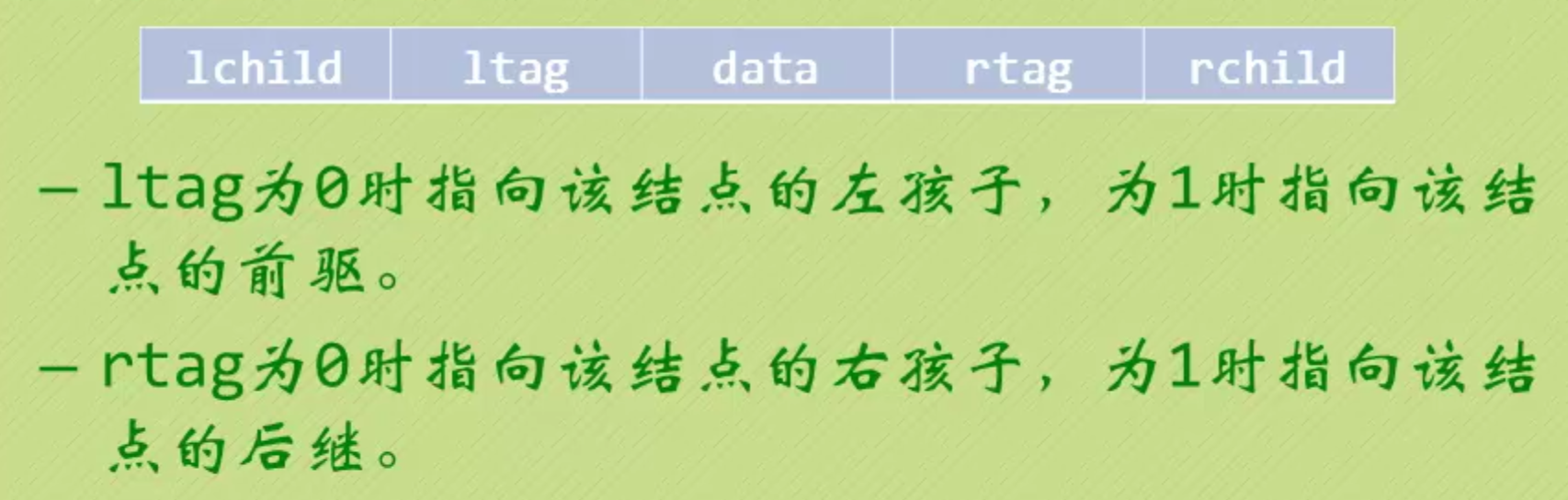
线索二叉树
普通的二叉树当结点没有孩子的时候就会空闲一个空间,为了可以将这个空间利用起来,并提高性能,创建出线索二叉树。
采用中序遍历法,可以大致得出每隔一个结点就会有一个空闲,可以利用这个空闲




树、森林及二叉树的转换
树转二叉树
- 在树中所有的兄弟结点之间加一条连线
- 对于每个结点,除去与其长子之间的连线外,去掉该结点与其他孩子之间的连线
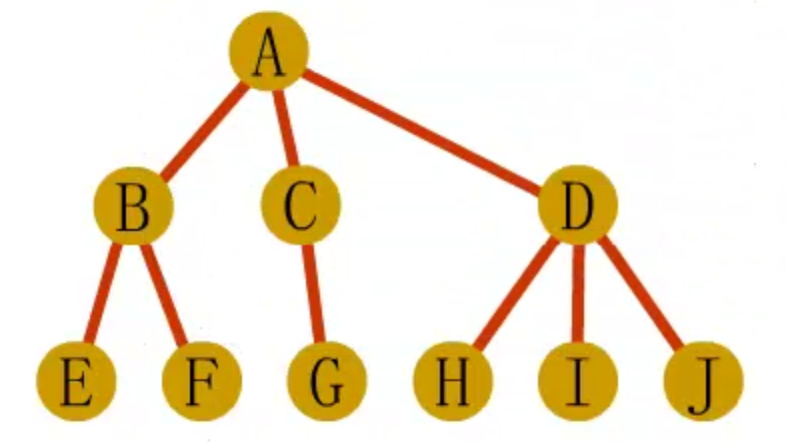
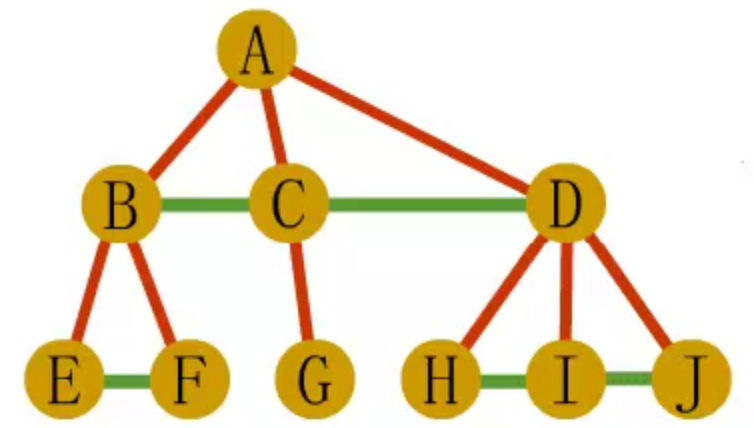
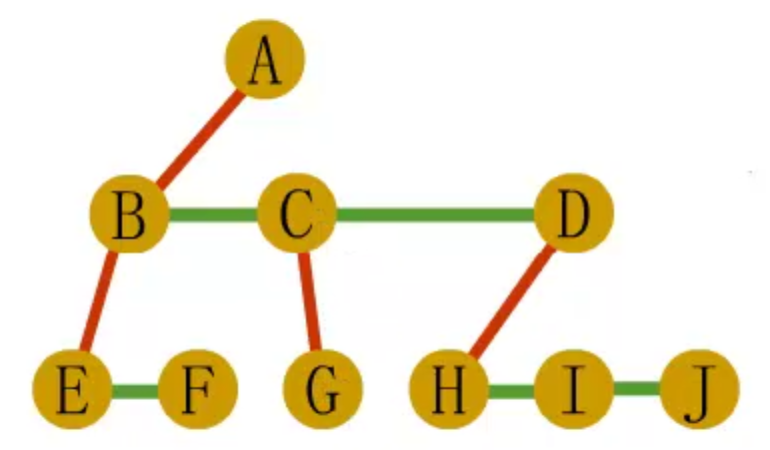
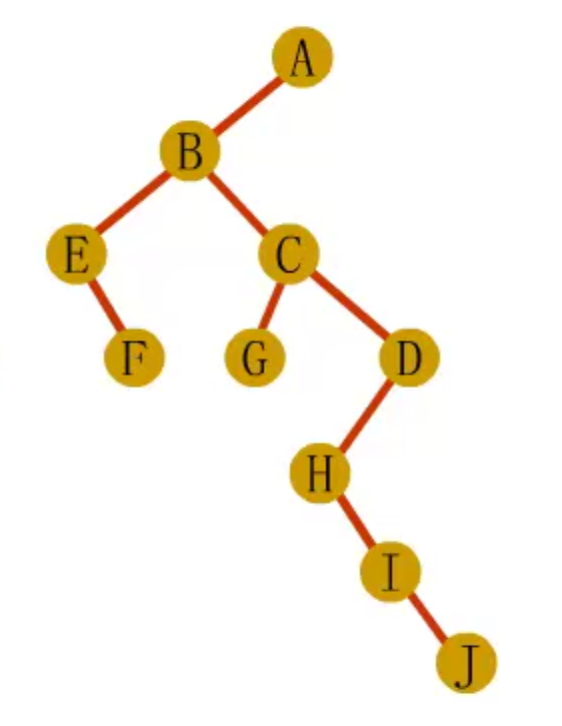
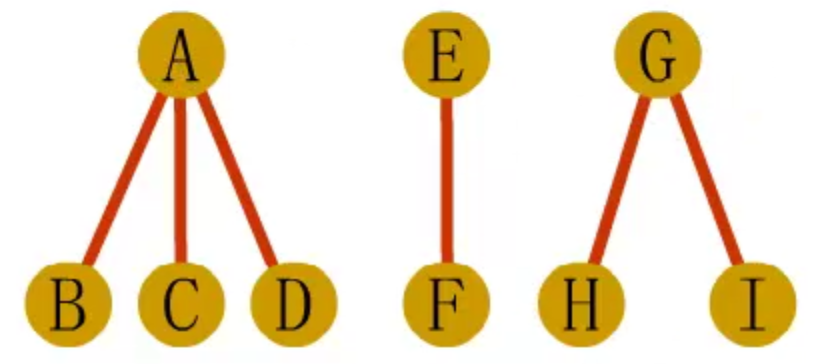
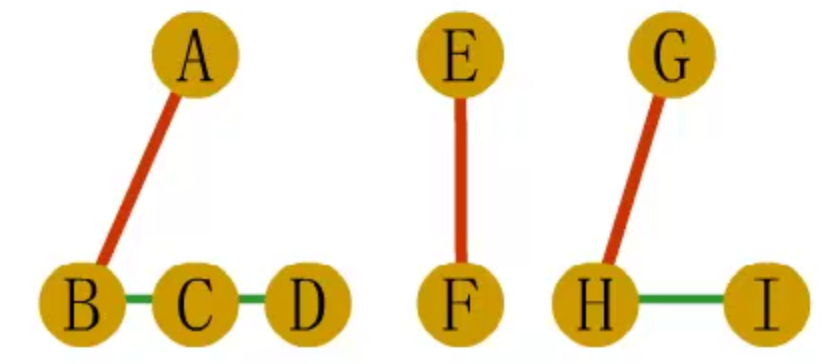
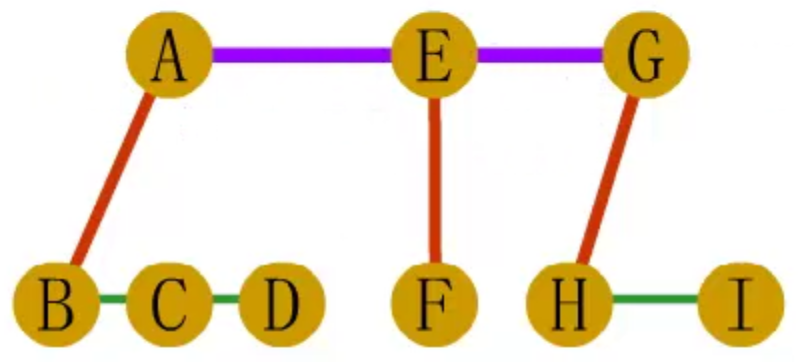
森林转二叉树
- 先将森林中的每棵树变成二叉树
- 再将各二叉树的根结点视为兄弟从左至右连在一起
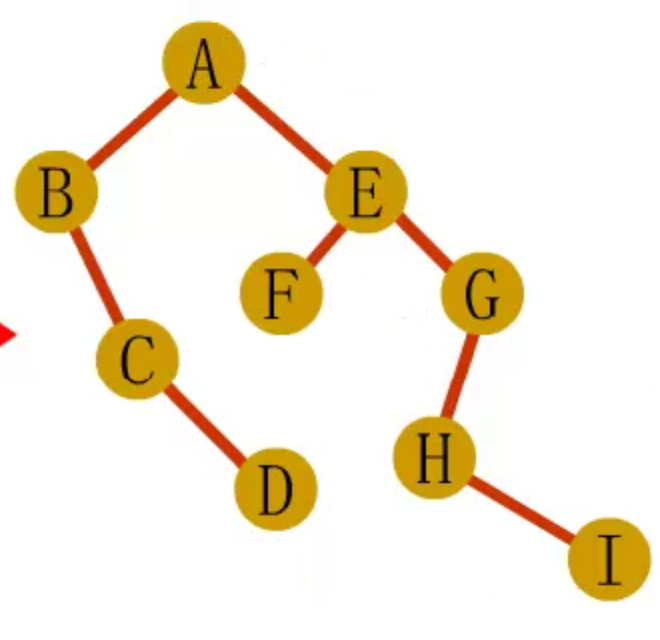
二叉树转森林、树
- 若结点x是其双亲y的左孩子,则把x的右孩子,右孩子的右孩子,。。。,都与y链接起来
- 去掉所有双亲到右孩子的连线
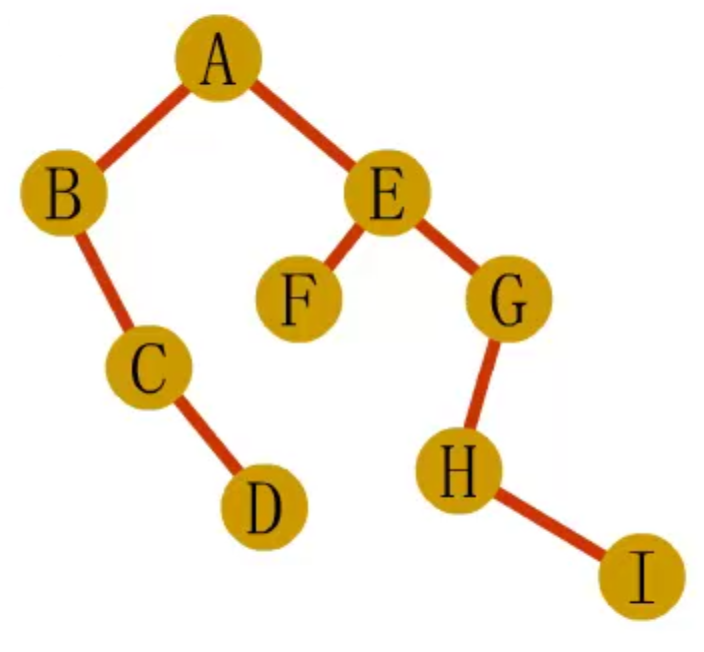
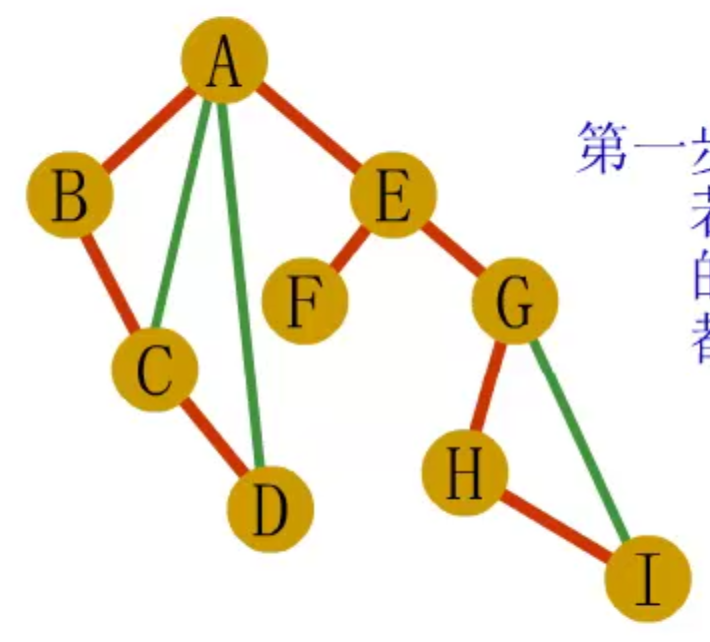
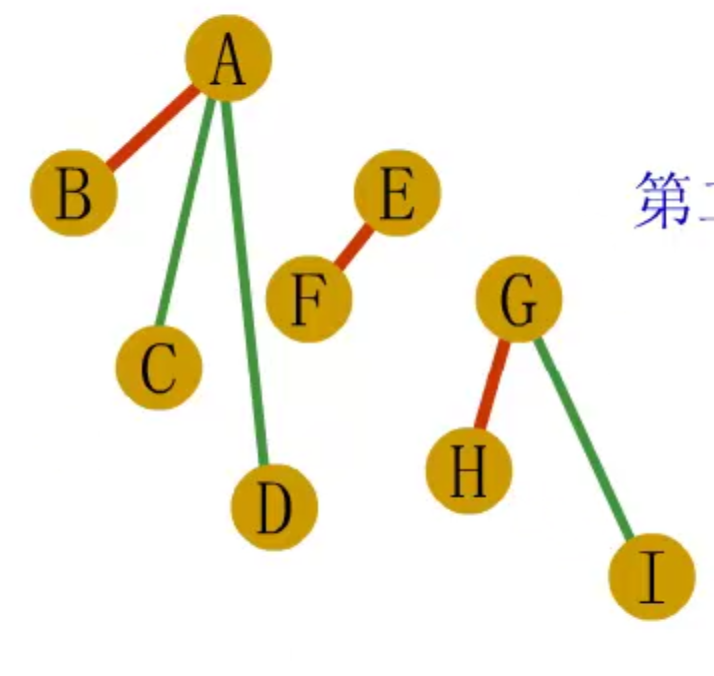
二叉树能够转换为树还是森林,看二叉树有没有右孩子,有就转换为森林,没有就转换为树
树的遍历
树的遍历分为先根遍历(先访问树的根结点,然后依次先根遍历每棵子树)和后根遍历(先依次遍历每棵子树,再访问树的根结点)。
先根遍历和二叉树的前序遍历结果相同,后根遍历和二叉树的中序遍历结果相同。
赫夫曼树
数据压缩,赫夫曼编码是首个实用的压缩编码方案,利用赫夫曼编码可以构造一种不等长的二进制,且不产生二义性。
权:树结点之间的连线相关的树。
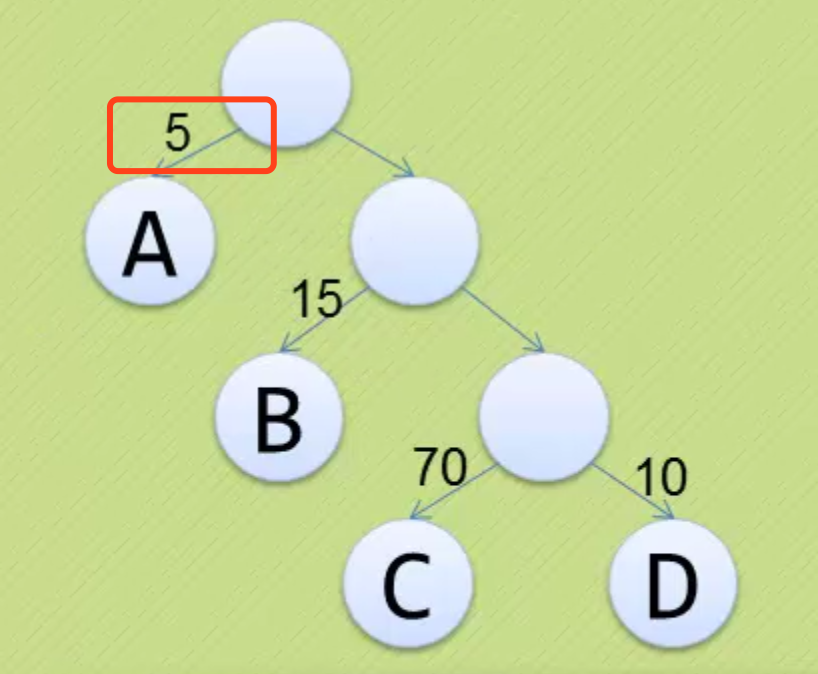
结点的路径长度:从根结点到该结点的路径上的连接数。
树的路径长度:树中每个叶子结点的路径长度之和。
结点带权路径长度:结点的路径长度与结点权值的乘积。
树的带权路径长度(WPL(Weighted Path Length)):树中所有叶子结点带权路径之和。
WPL的值越小,说明构造出的二叉树性能越优,性能最好的二叉树就是赫夫曼树。
赫夫曼树的构造过程:
- 取出所有数据中两个权值最小的两个结点,小的放左边,大的放右边,然后创建这两个结点的父节点,父节点的权值为这两个结点之和。
- 在剩余的数据中取出权值最小的结点与上生成的结点比较,小放在左边,大放在右边,再次生成这两个结点的父节点,然后重复进行上述操作
赫夫曼编码
赫夫曼编码可以有效压缩数据的20%-90%。
定长编码、变长编码、前缀码(没有任何码字是其他码字的前缀)
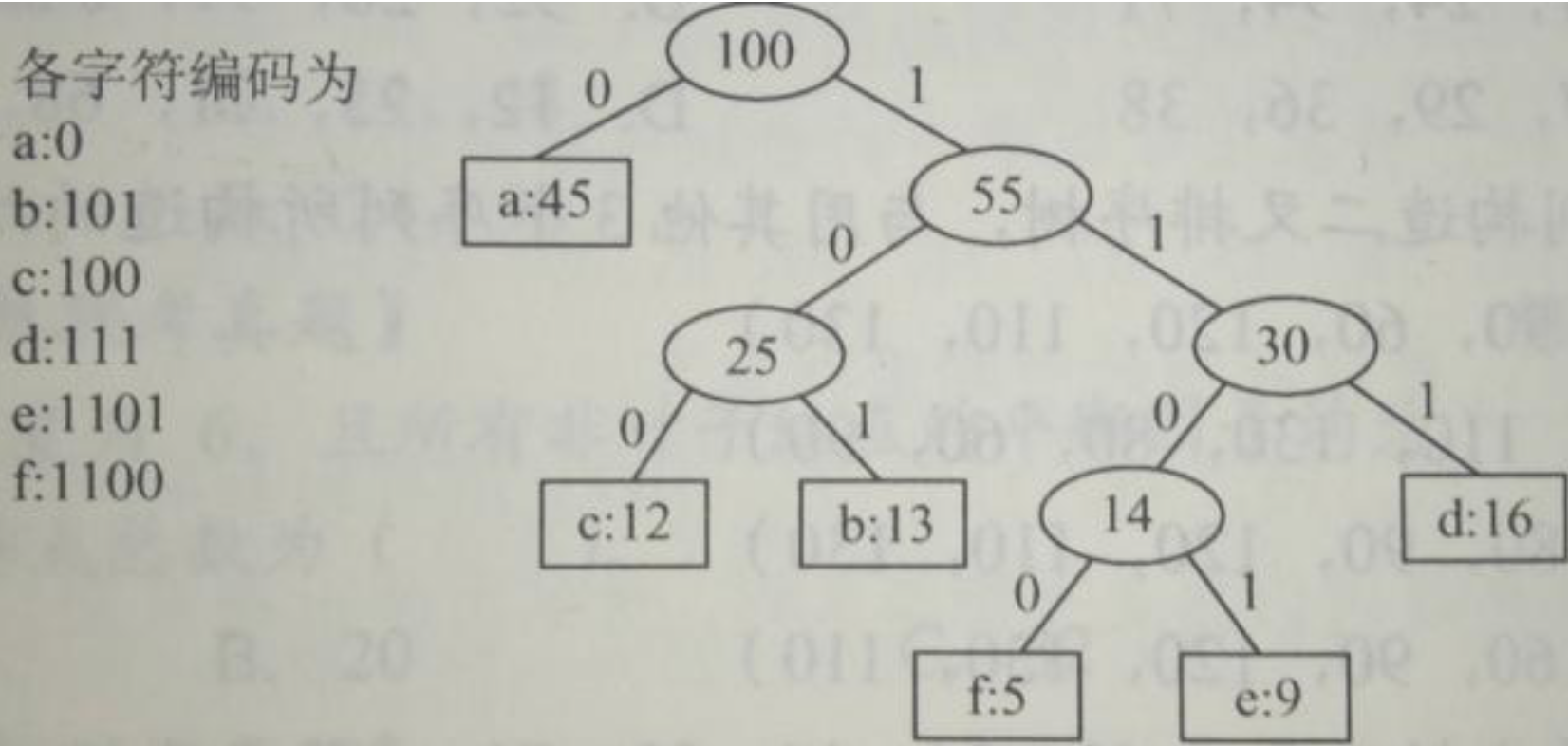
如上图,左子树都是0,右子树都是1。