概要
图(Graph):是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中G表示图,V表示图G中顶点的集合,E表示图G中边的集合。
无向边:若顶点Vi到Vj之间的边没有方向,则称这条边为无向边,用无序偶(Vi,Vj)或(Vj,Vi)来表示。
有向边:若顶点Vi到Vj之间的边有方向,则称这条边为有向边,也称弧,用有序偶<Vi,Vj>来表示,Vi称为弧尾,Vj称为弧头。
简单图:在图结构中,若不存在顶点到其自身的边,且同一条边不重复出现,称该图为简单图。
无向完全图:在无向图中,如果任意两个顶点之间都存在边,则称无向完全图。含有n个顶点的无向完全图有n * (n-1) / 2条边。
有向完全图:在有向图中,如果任意两个顶点之间都存在方向互为相反的两条弧,则称有向完全图。含有n个顶点的无向完全图有n * (n-1)条边。
稀疏图和稠密图:这是两个相对的概念,通常将弧数小于n*logn(n为顶点数)的图称为稀疏图,反之称为稠密图。
权和网:图中边或弧带有数字,这个数字称为权,带权的图称为网。
子图:假设有两个图G1=(V1, E1)和G2=(V2, E2),如果V2⊆V1,E2⊆E1,称G2为G1的子图。
顶点的度:与顶点V相关联的边的数目。
无向图邻接点:对于无向图G=(V, E),如果边(V1, V2) ∈ E,则称顶点V1和V2互为邻接点,边(V1, V2)依附于顶点V1和V2。
有向图邻接:对于有向图G=(V, E),如果边<V1, V2> ∈ E,则称顶点V1邻接到顶点V2。
入度和出度:以顶点V为头的弧的数目称为V的入度,记为ID(V);以顶点V为尾的弧的数目称为V的出度,记为OD(V),顶点V的度TD(V)=ID(V)+OD(V);
路径:从顶点V1到顶点V2之间称为路径,路径上边的数目称为路径的长度。
简单环:序列中顶点不重复出现的路径称为简单路径,除了第一个和最后一个顶点外,其余顶点都不重复出现的回路称为简单环。
连通图:在无向图中,如果从顶点V1到顶点V2有路径,则称V1和V2是连通的,如果对于图中任意两个顶点都是连通的,则称为连通图。
连通分量:无向图中的极大连通子图称为连通分量。
强连通图:在有向图中,如果每一对V1和V2都存在路径,则称为强连通图。
强连通分量:有向图中的极大连通子图称为强连通分量。
连通图的生成树:是一个极小连通子图,包含图中全部的n个顶点,但只有足以构成一棵树的n-1条边。
有向图:如果一个有向图,恰有一个顶点的入度为0,其余顶点的入度为1,则是一棵有向树。
图的存储结构
邻接矩阵
图是由顶点和弧组成,用两个部分存储图,用一维数组存储顶点(无分位置、大小),用二维数组存储弧(有弧为1,无弧为0)。
- 无向图(邻接矩阵):是一个对称矩阵,顶点V1的度为V1列或V1行的数据之和。
- 有向图(邻接矩阵):顶点V1的入度为V1列数据之和,出度为V1行数据之和。
- 网(邻接矩阵):对应的值为其权值
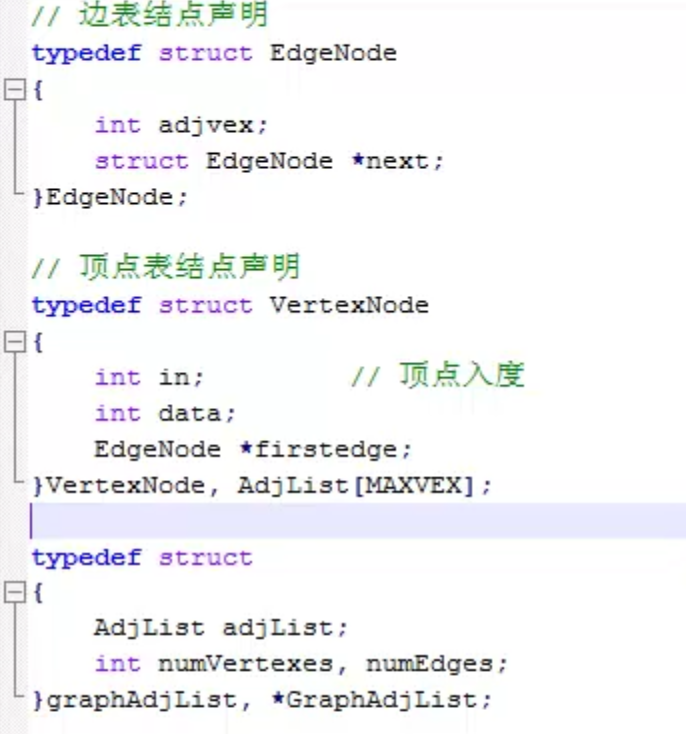
邻接表(节省存储空间)
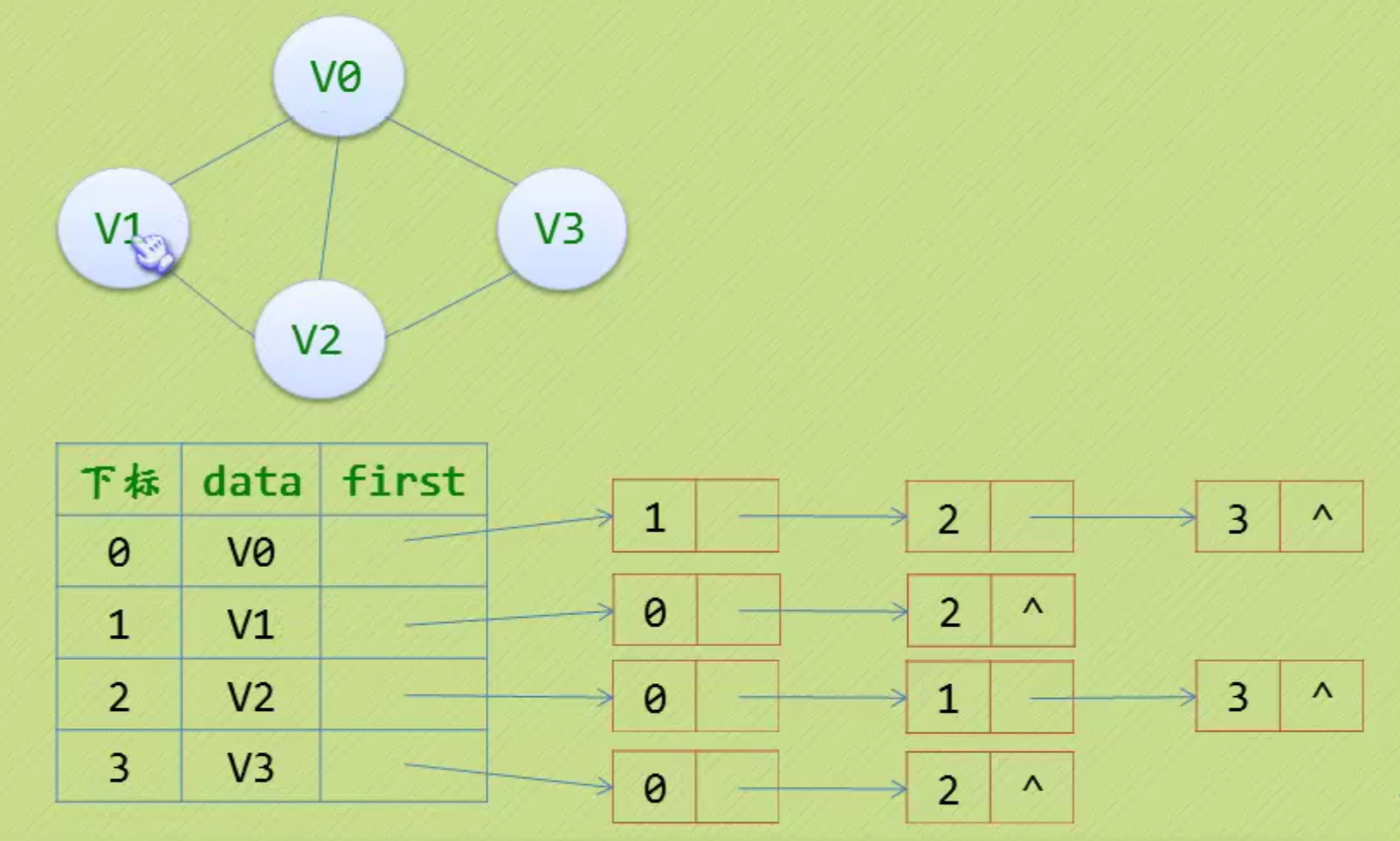
- 无向图的邻接表:
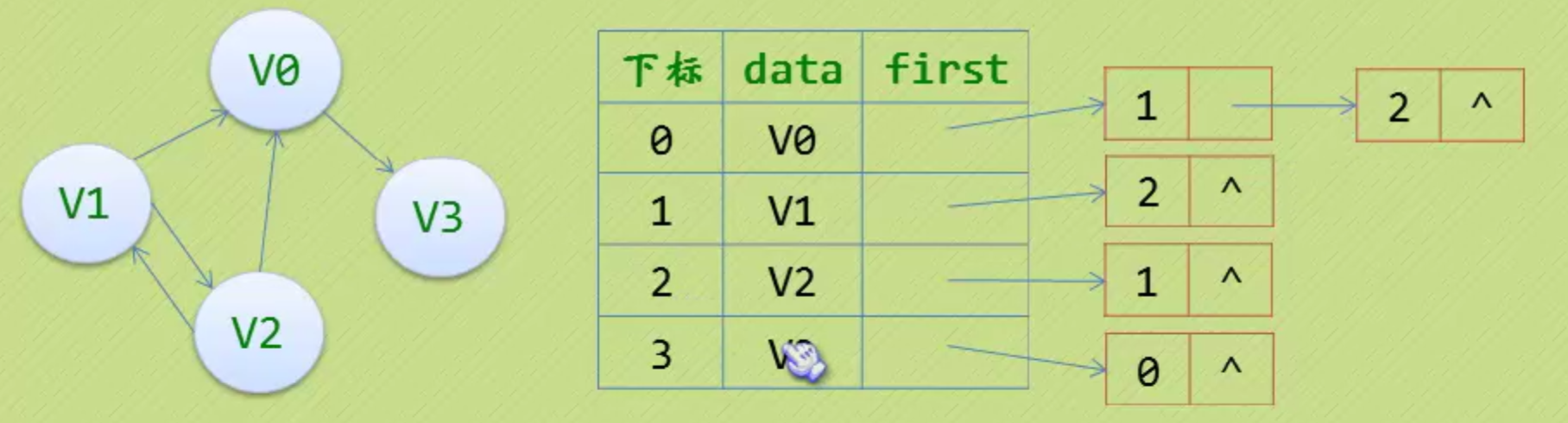
- 有向图的邻接表:可以方便的算出顶点出度
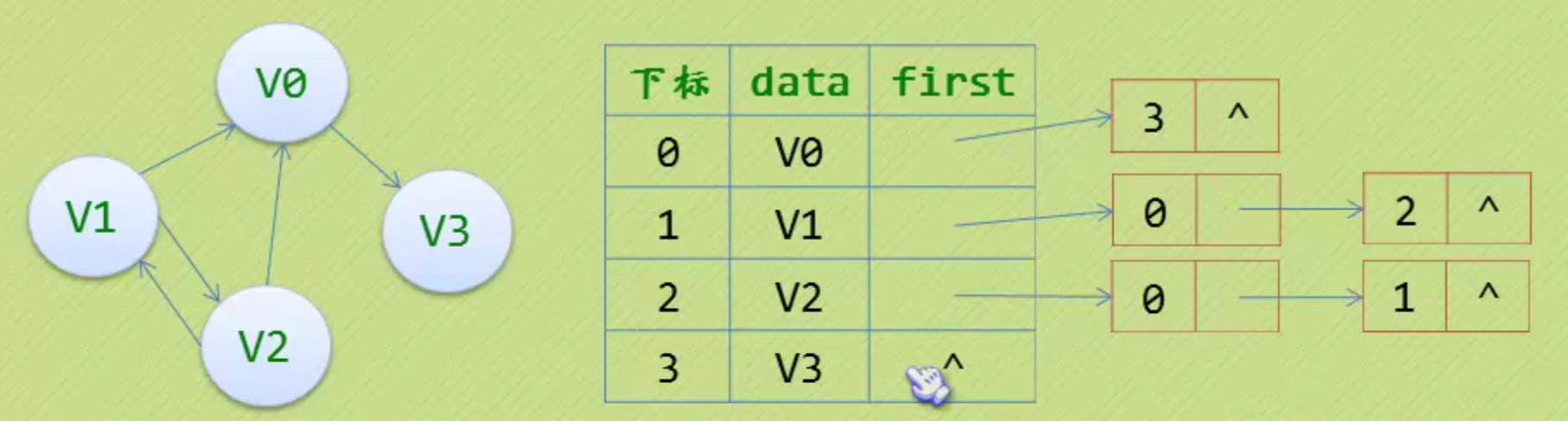
- 有向图的逆邻接表:可以方便的算出顶点入度
- 网的邻接表:增加一个数据域
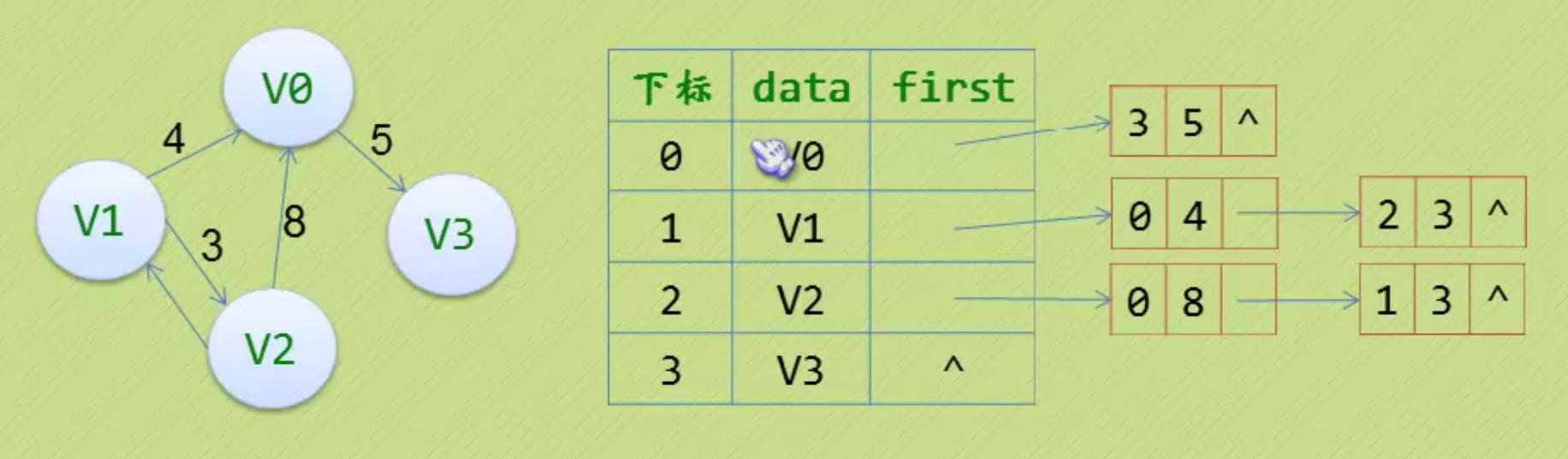
十字链表:将邻接表和逆邻接表组合起来(主要针对有向图进行存储优化)


邻接多重表(针对无向图优化)
对于无向图中,如果删除一条边,则会设计多出修改,非常不方便。

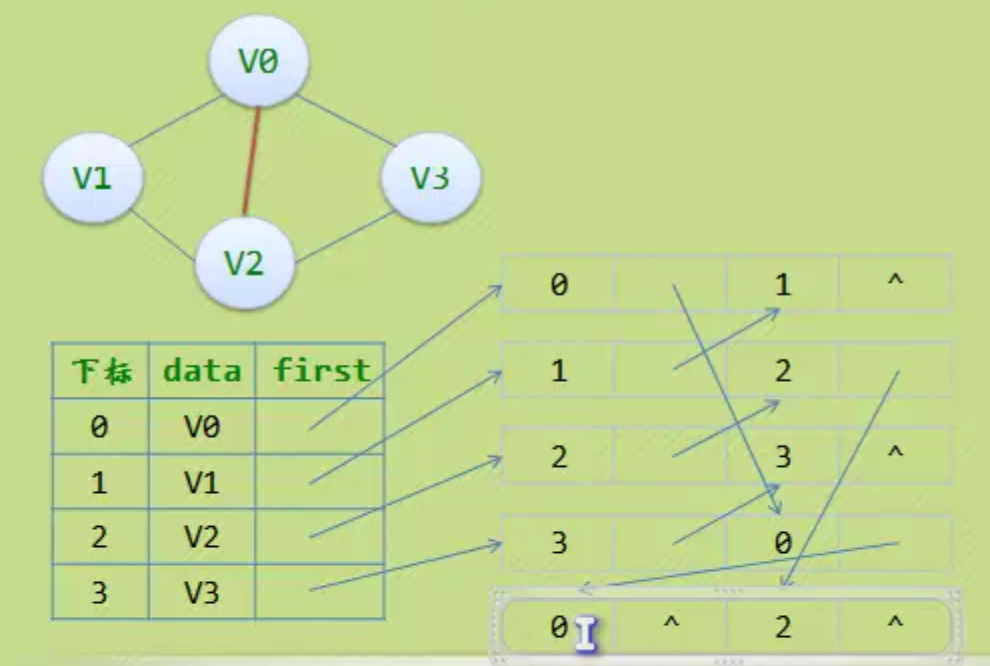
边集数组
由两个一维数组组成,一个存储顶点信息,另一个存储边的信息(包括边的起点下标、终点下标、权)
深度优先遍历
根据左手或右手原则,向下遍历,遍历过得添加一个标记,直到终点,然后回退比较,直至开始(递归的过程)。类似树的前序遍历
广度优先遍历
类似树的层序遍历
最小生成树
普利姆算法(针对顶点展开,适用稠密图)
- 初始化权值数组为第0行的所有权值
- 取出最小权值所在的列值k,并将其作为下一个权值取值的行,并将权值数组中此权值设置为0
- 将第k行的权值与权值数组中的权值依次比较,将第k行权值小的代替原权值数组的值
- 循环执行第2步,至遍历完全部的顶点
克鲁斯卡尔算法(针对边展开,适用稀疏图)
- 所有边按权值大小升序排序
- 从小大取出,检测是否构成环路,否,则选择,是,则跳过
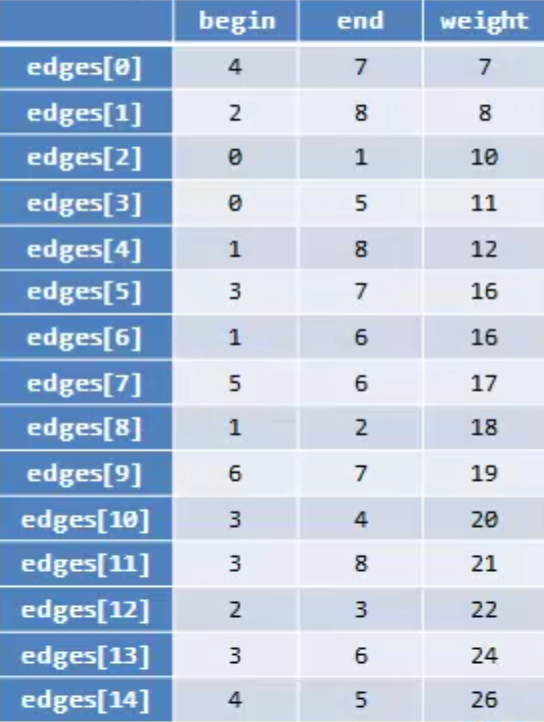
最短路径
- 在网图中两顶点经过边上权值之和最少的路径
- 在非网图两顶点之间经过边数最少的路径
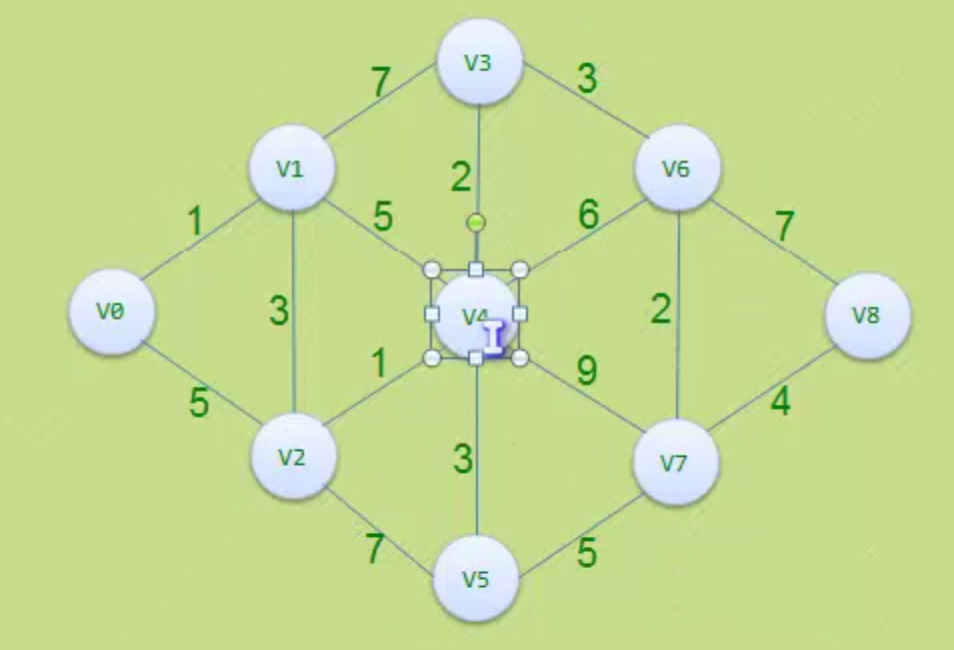
迪杰斯特拉算法(一个顶点到所有顶点的最短路径)
- 初始化最短路径数组(D)为第0个顶点到其他顶点的所有权值,标志位数组(F)全为0,除第一个外(权值为0,标志位1)
- 从1开始到终点依次遍历执行以下步骤
- 初始化最小值为INF
- 遍历所有顶点取出标志位为0且权值小于最小值的下标(k)和权值(min)
- 设置下标为k的标志位为1
- 遍历第k行顶点权值,找出标志位为0且下一个路径权值和小于当前权值的顶点位置,覆盖当前权值
弗洛伊德算法(所有顶点到所有顶点的最短路径)
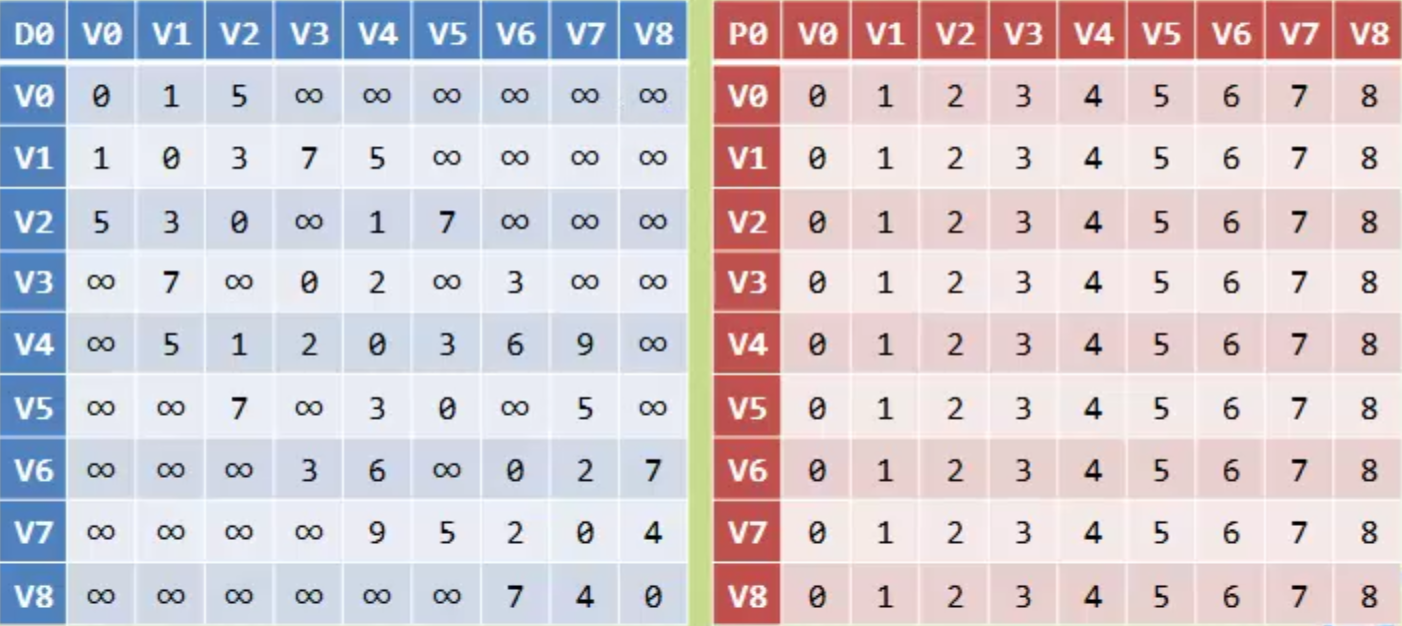
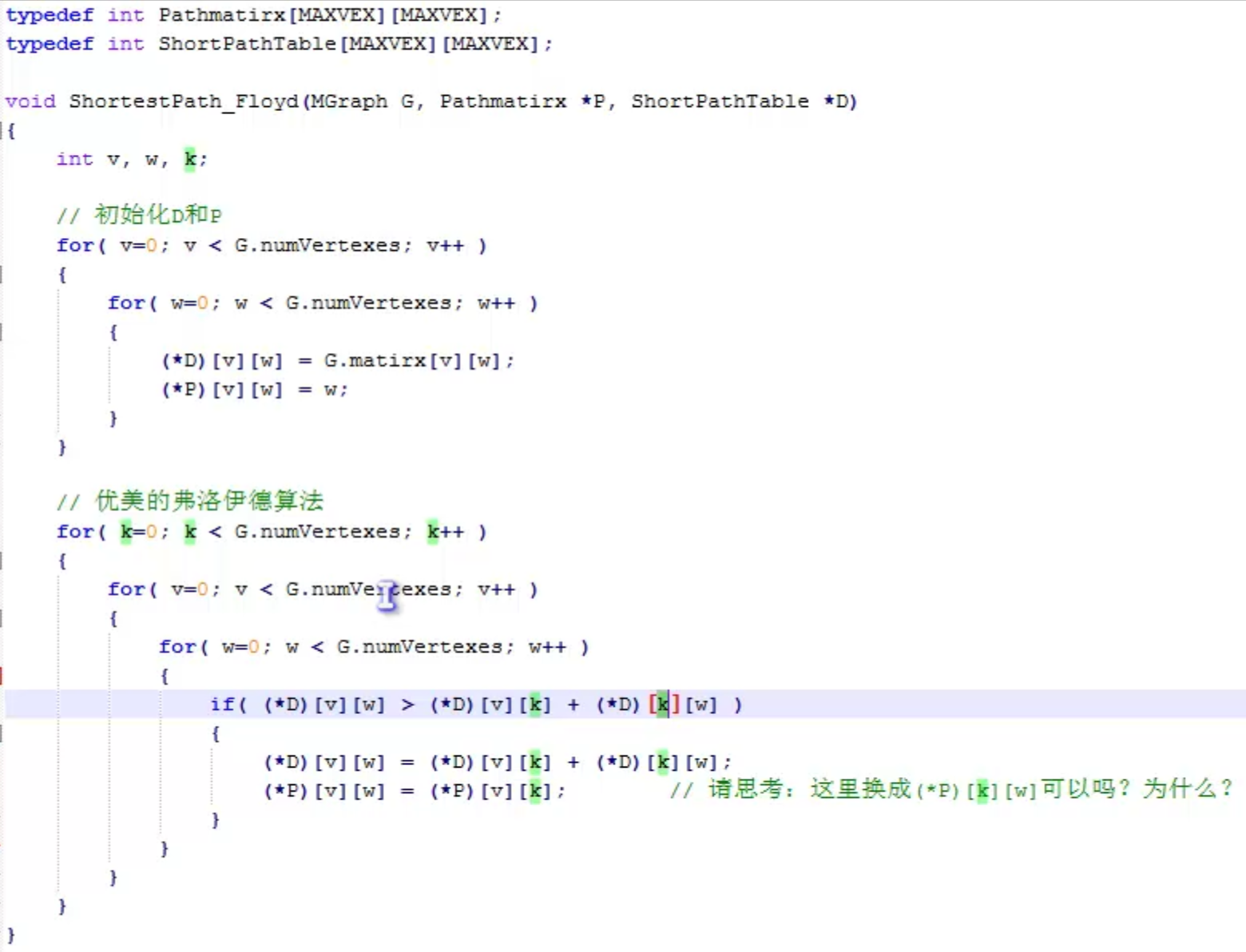
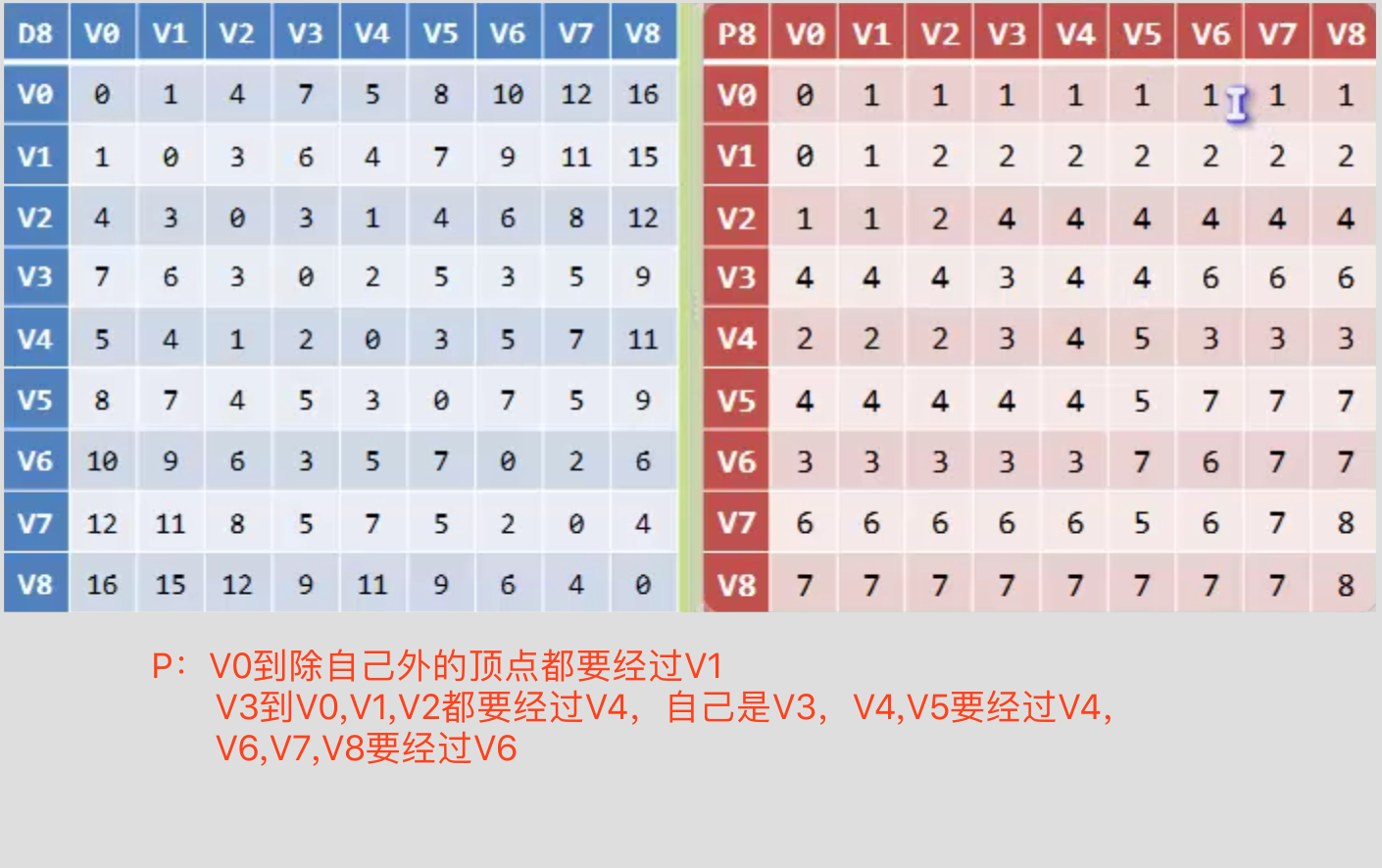
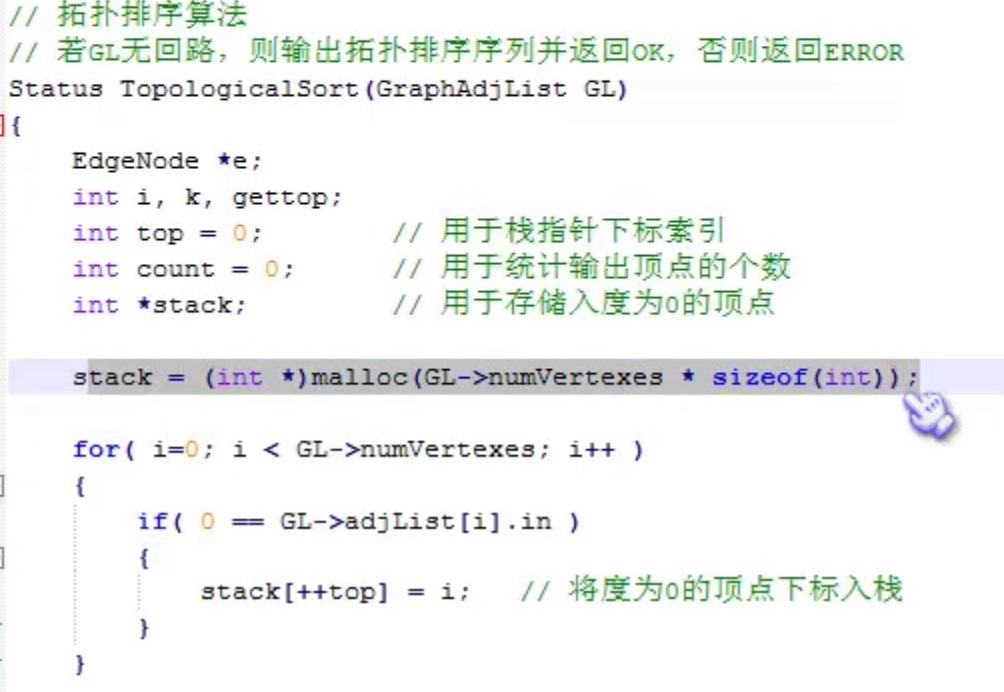
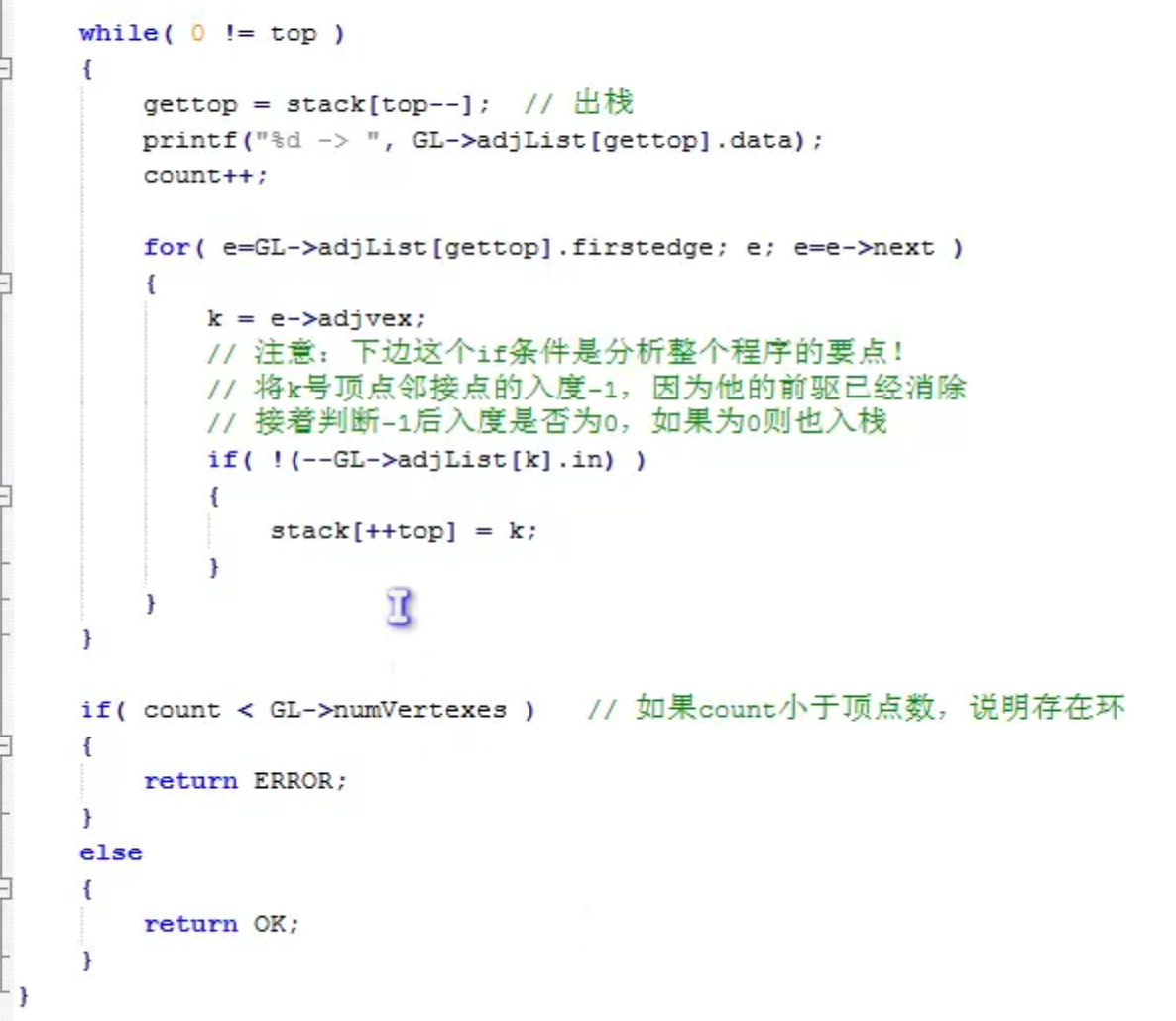
拓扑排序
一个无环的有向图称为无环图,简称DAG图。
所有的工程或流程都可以分为若干个小的流程或阶段,称之为“活动”。
在一个表示工程的有向图中,顶点表示活动,弧表示活动之间的优先关系,这样的有向图为顶点表示的活动的网,称为AOV网,不能存在环。
拓扑序列:设G=(V,E)有一个具有n个顶点的有向图,V中的顶点序列V1,V2,…Vn满足若从Vi到Vj有一条路径,则在顶点序列中顶点Vi必在Vj之前,则称这样的顶点序列为拓扑序列。
拓扑排序:对一个有向图构造拓扑序列的过程。
对AOV网进行拓扑排序的过程:
- 从AOV网中选择一个没有前趋的顶点,该顶点的入度为0
- 从网中删除该顶点,并删除从该顶点出发的所有边
- 重复上述两步,直到网中没有前趋的顶点为止
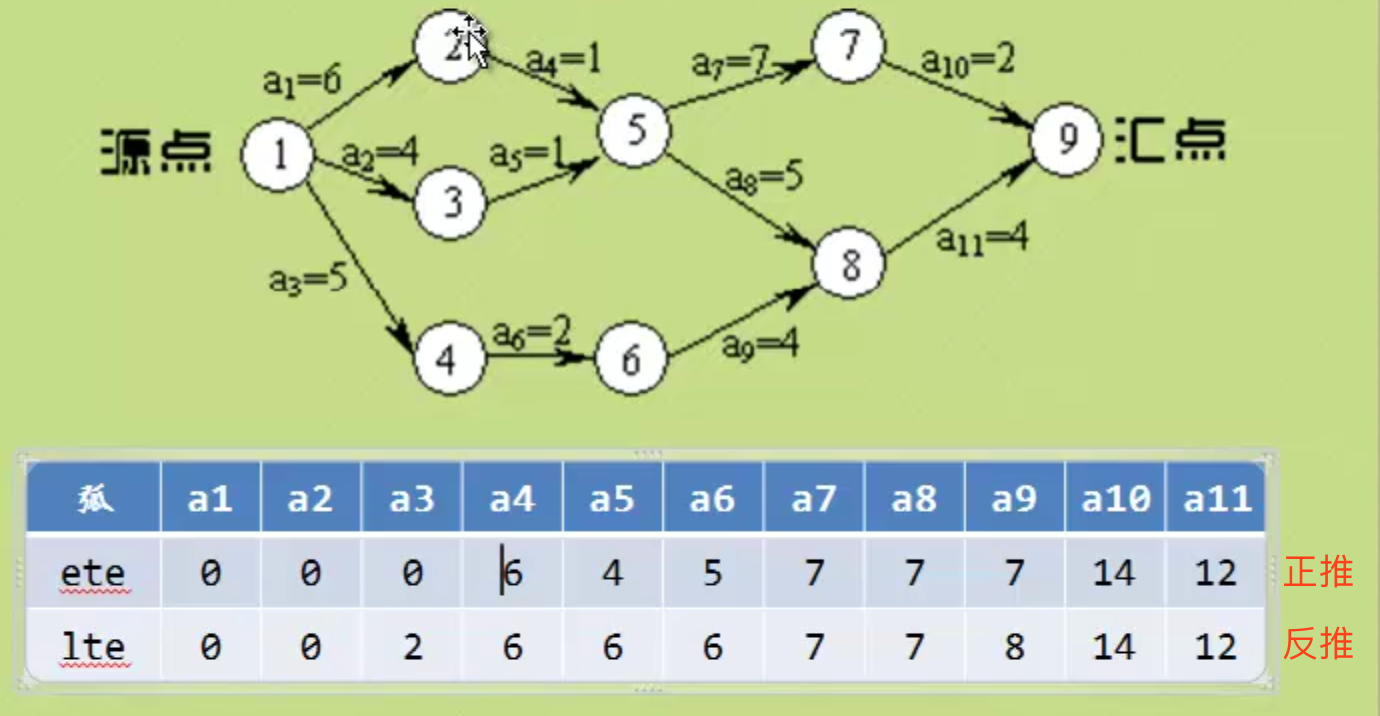
关键路径
在一个表示工程的带权有向图中,顶点表示事件,有向边表示活动,权值表示活动的持续时间,这种有向图的边表示的活动的网,称为AOE网。
- etv(Earliest Time of Vertex):事件(顶点)发生最早时间
- ltv(Latest Time of Vertex):事件(顶点)发生最晚时间,晚于这个时间会延误工期
- ete(Earliest Time of Edge):活动(边)发生最早时间
- lte(Latest Time of Edge):活动(边)发生最晚时间,晚于这个时间会延误工期
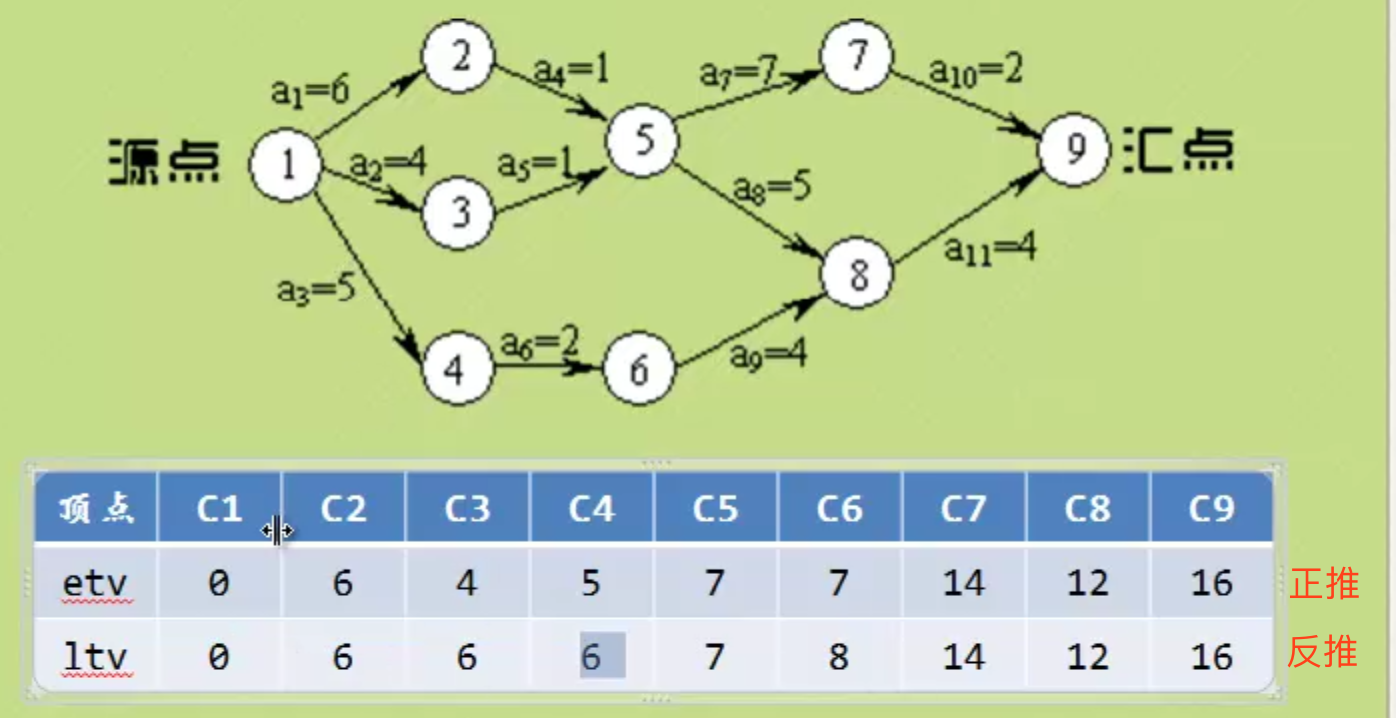
etv = ltv的顶点就是关键路径。