概要
查找分为静态查找和动态查找。
- 静态查找：数据集合稳定，不需要添加删除元素
- 动态查找：数据集合在查找过程中需要同时添加或删除元素
静态查找
顺序查找
按照顺序进行比对，相等就是查找结果，不相等就没有结果。
时间复杂度：O(n)。
插值查找（按比例查找）
在折半查找的基础上，按比率进行查找，适用于数据量大且分布均匀的数据，否则效率低于折半查找。
mid = low + ((key - a[low]) / (a[high] - a[low])) * (high - low);
时间复杂的：O(logn)。
斐波那契查找（黄金比例）
斐波那契数列(a(n) = a(n-1) + a(n-2)): 1，1，2，3，5，8，13，21，…
后二数之比2/3，3/5，5/8，8/13，13/21，… 无限接近黄金比例（0.618）。
将源数据的个数映射到斐波那契数列中，根据斐波那契数列的特性对源数据进行分割查找比较，即比例为0.618的插值查找。
时间复杂的：O(logn)。
线性索引查找
为数据建立已排序索引表，根据索引表查找数据。
稠密索引
建立和数据相同当量的索引表，适用于数据量不是很大的场景。
分块索引
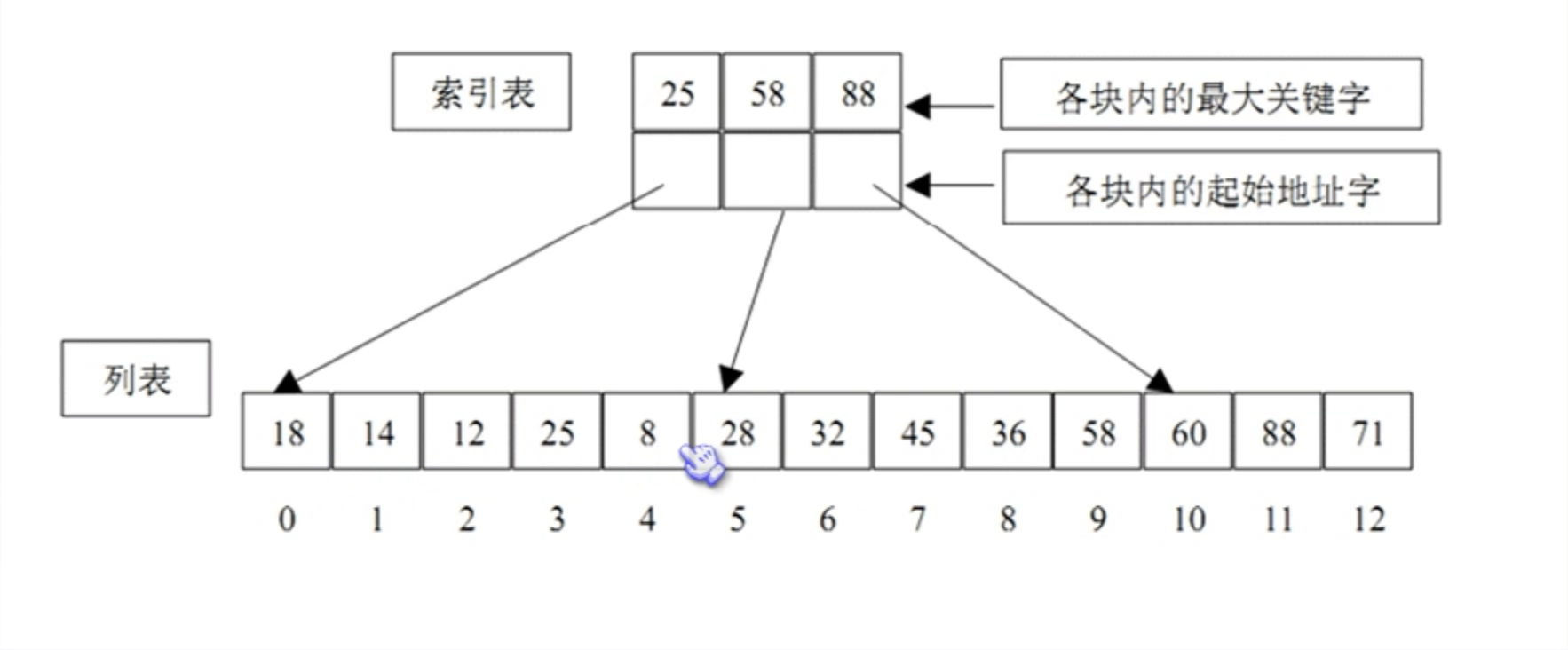
倒排索引
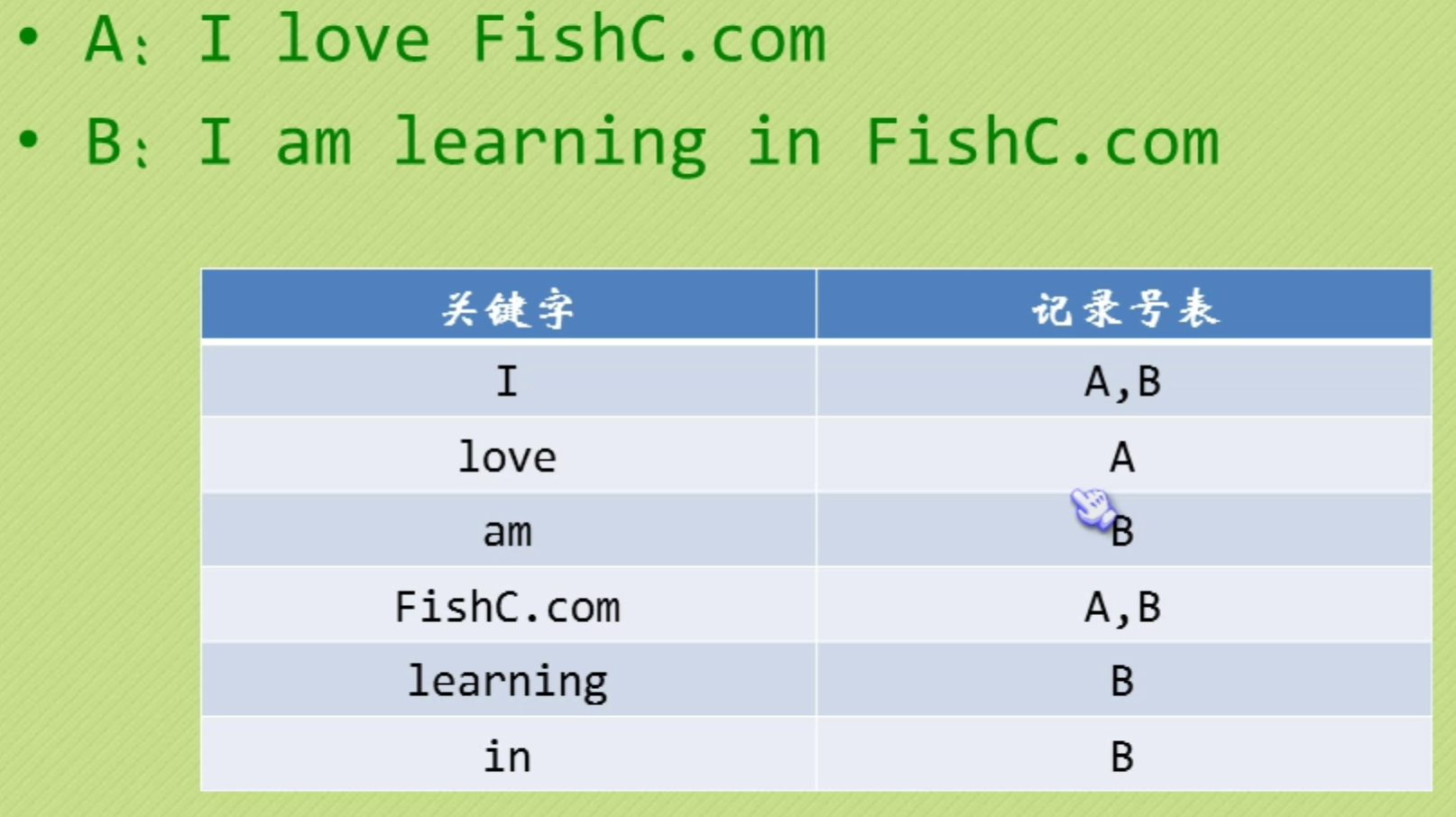
二叉排序树（二叉查找树）
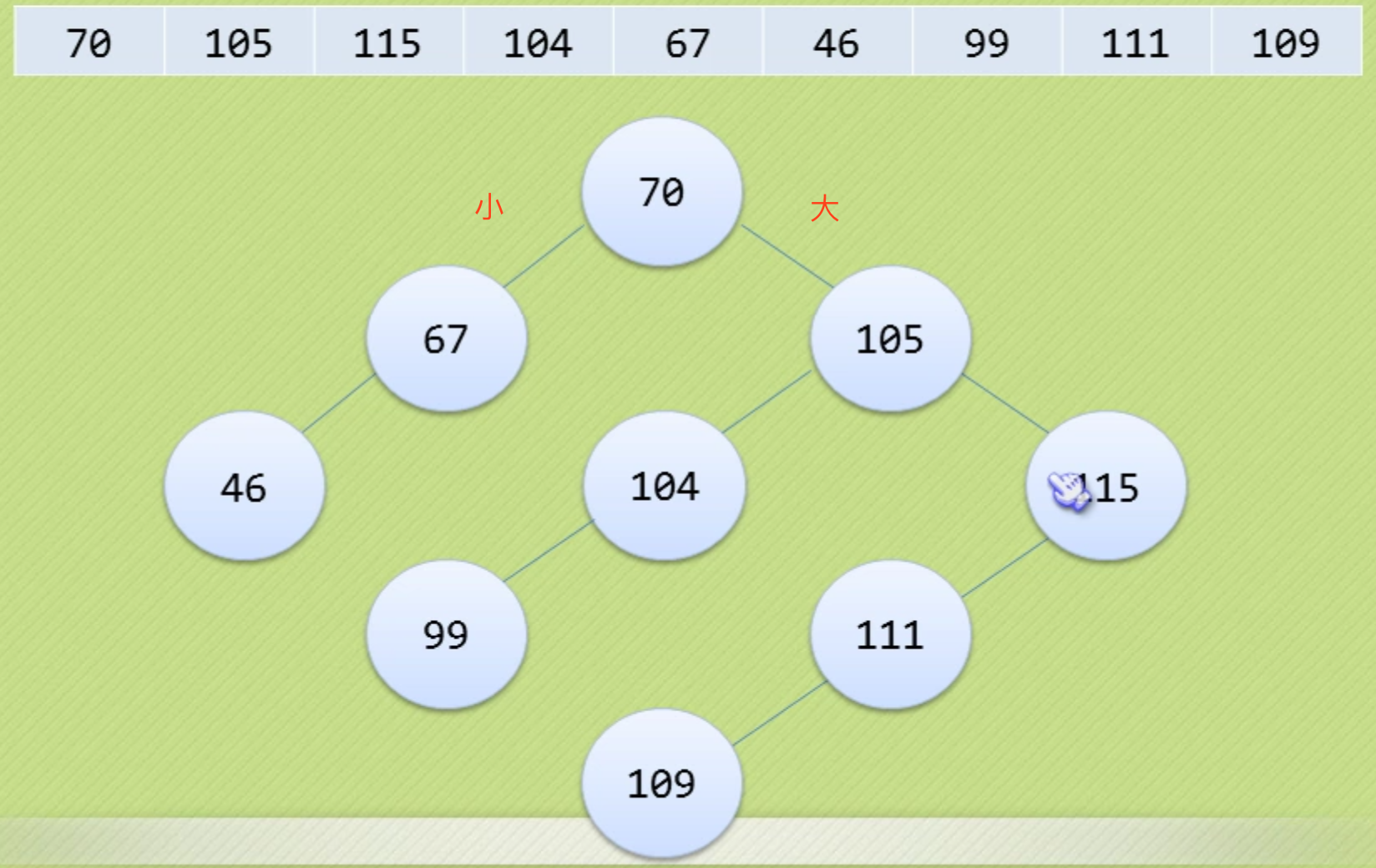
二叉排序树性质：
- 左子树上所有结点的值均小于他的根结构的值
- 右子树上所有结点的值均大于他的根结构的值
- 左、右子树也分别为二叉排序树（递归）
二叉排序树查找
二叉排序树插入
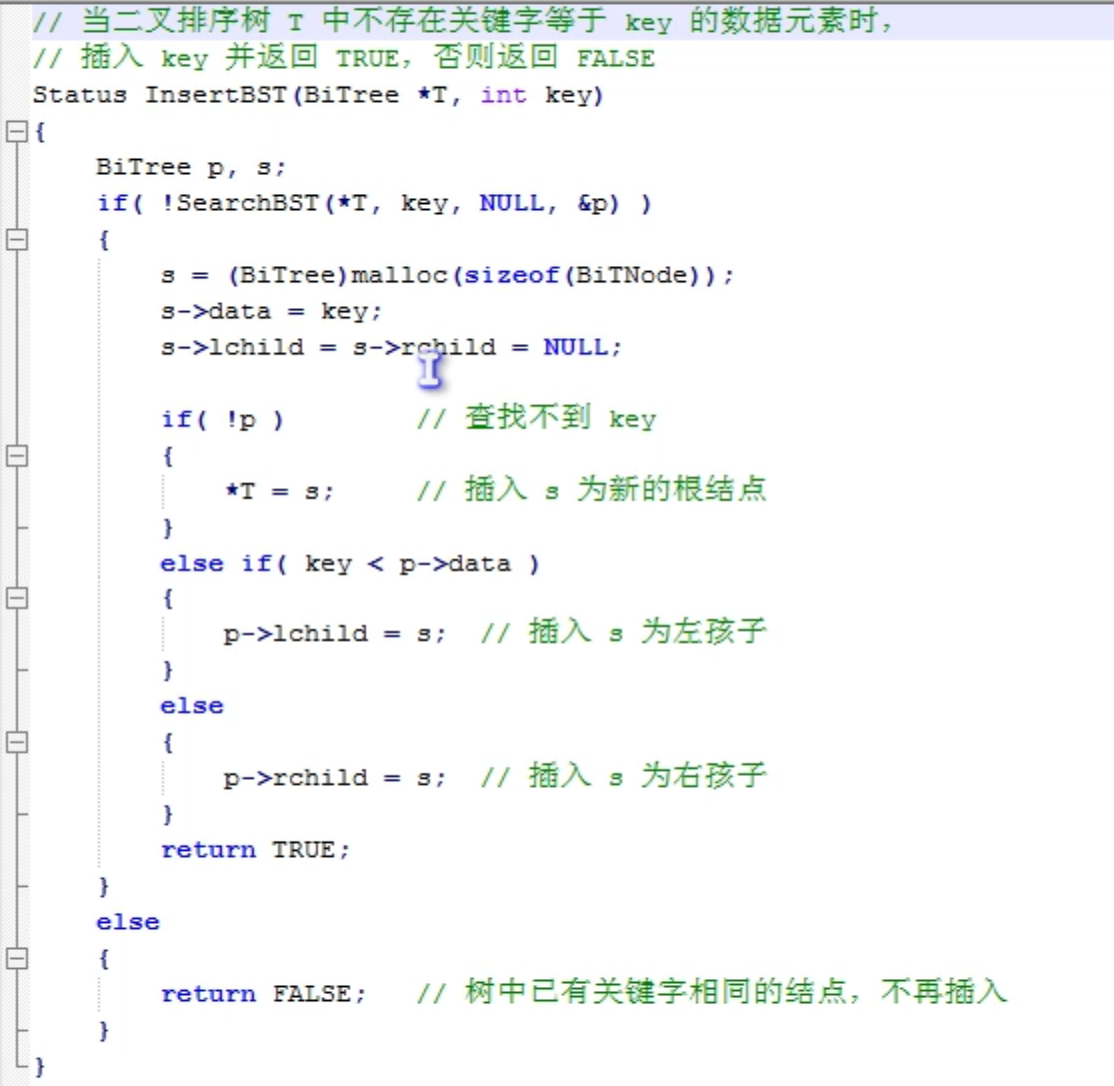
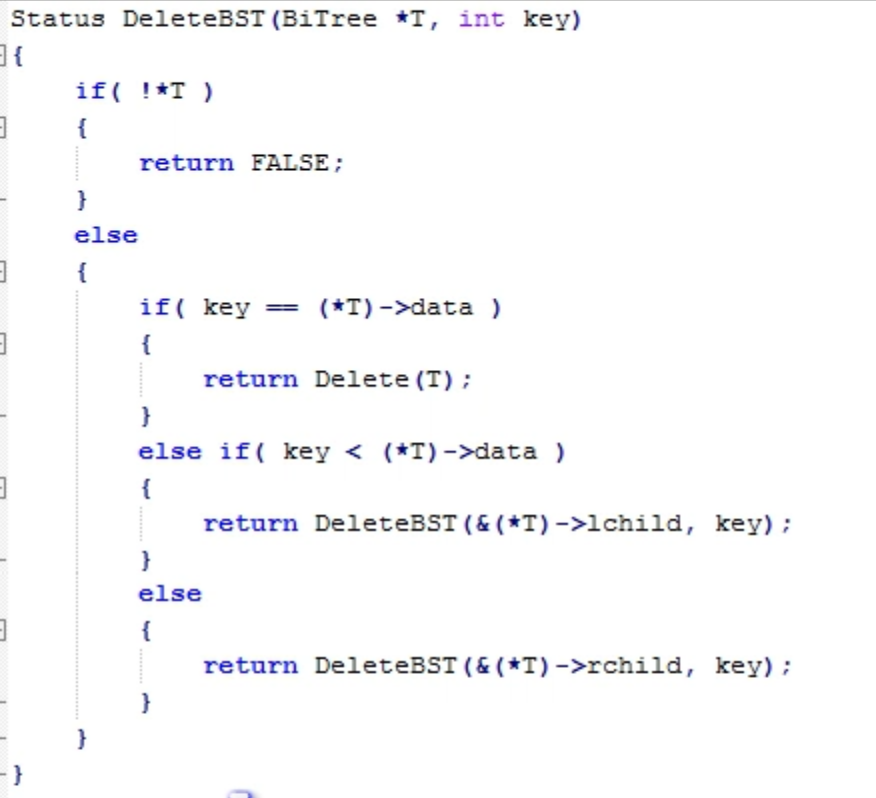
二叉排序树删除
- 如果该结点是叶子结点，直接删除
- 如果该结点只有左子树或右子树，直接删除，然后接上
- 如果既有左子树又有右子树，采用中序排序找到其前驱或后继替换，然后接上
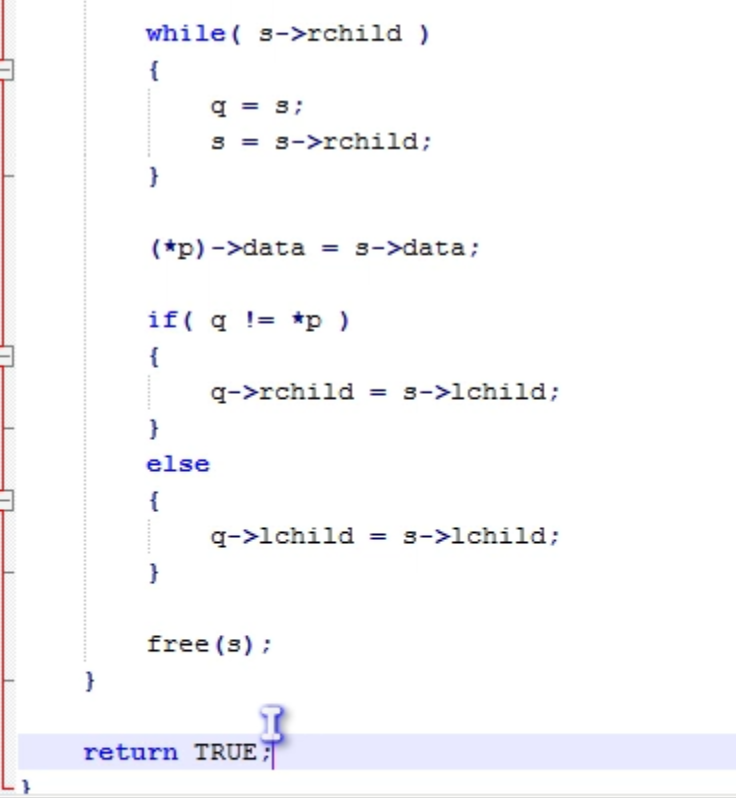
平衡二叉排序树
平衡二叉排序树的特点：
- 左子树和右子树都是平衡二叉树
- 左子树和右子树的深度只差（平衡因子BF）的绝对值不超过1
插入，查找，删除的时间复杂度最好情况和最坏情况都维持在O(logN)。
演示一组数据怎么组成一棵AVL树。
int a[] = {4,3,2,7,9,11,10};
- 插入4，如图：
，平衡因子为0. - 插入3，如图：
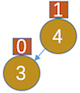，4的平衡因子因为4的左子树增长了，1-0=1 - 插入2，如图：
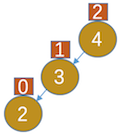，显然4的平衡因子大于1了，为了保持平衡那我们就这样做：让4节点的左孩子指向3的右子树（此时为NULL），让3的右孩子指向4，让树根指向3，如图
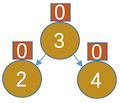，这种操作我们规定为右旋操作。 - 插入7，如图：
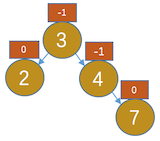
- 插入9，如图：
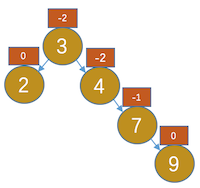，显然节点4不平衡了。那我们就把4的右孩子7的左子树（此时为NULL），让7的左孩子指向4，让3的右孩子指向7，如图：
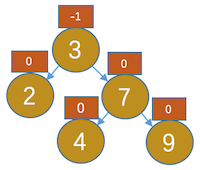，我们规定此操作为左旋操作，此图是以4为根进行旋转。 - 插入11，如图：
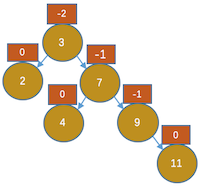，显然3节点，不平衡了，大家都应该知道以3为根进行左旋。让3的右孩子指向7的左子树（此时为4）。7的左孩子指向3，根指向7，如下图所示：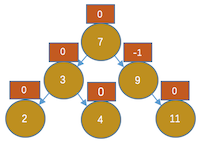
- 插入10，如图：
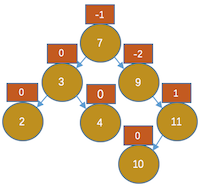，显然节点9不平衡，且是右边高，那我们左旋吧，左旋后的效果是上图右图所示。显然这是不对的，10比11小，但在11的右孩子上。（根本原因是9和11的平衡因子符号不同）那我们在怎么办呢,看下图吧：
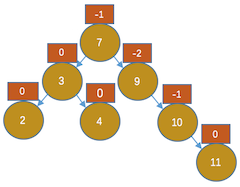，以11为根先右旋，
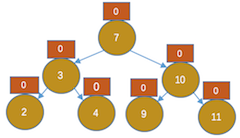，再以9为根左旋。
#define EH 0 // 等高
#define LH 1 // 左高
#define RH -1 // 右高
typedef struct _BitNode
{
int data;
int bf; //平衡因子
struct _BitNode *lchild, *rchild;
} BitNode, *BiTree;
void R_Rotate(BiTree *T)
{
BiTree p;
p=T->lchild; // 假如此时T指向4，则p指向3；
T->lchild=p->rchild; // 把3的右子树挂接到4的左子树上（此例子3右子树为空）
p->rchild=T; // 让3的右孩子指向4.
T=p; // 根指向节点3
}
void L_Rotate(BiTree *T)
{
BiTree p;
p=T->rchild; //假如此时T指向4，则p指向7.
T->rchild=p->lchild; //让7的左子树挂接到4的右子树上
p->lchild=T; //让7的左孩子指向4
T=p; //树根指向7
}
void RightBalance(BiTree *T)
{
BiTree R,rl; //调用此函数时，以T为根的树，右边高于左边，则T->bf=RH。
R=T->rchild; //R是T的右孩子
switch (R->bf)
{
case RH: //如果T的右孩子和T他们的平衡因子符号相同时，则直接左旋，这是总结中的第2项
T->bf=R->bf=EH;
L_Rotate(T);
break;
case EH:
T->bf=RH;
R->bf=LH;
L_Rotate(T);
break;
case LH: //如果T的右孩子和T他们的平衡因子符合不同时，需要先以T的右孩子为根进行右旋，再以T为根左旋。
//rl为T的右孩子的左孩子
rl=R->lchild; //2次旋转后，T的右孩子的左孩子为新的根 。注意：rl的右子树挂接到R的左子树上，rl的左子树挂接到T的右子树上
switch (rl->bf) //这个switch 是操作T和T的右孩子进行旋转后的平衡因子。
{
case EH:
T->bf=R->bf=EH; //这些平衡因子操作，大家可以自己画图操作理解 下面的注解
break;
//2次旋转后，T的右孩子的左孩子为新的根 。
//并且rl的右子树挂接到R的左子树上，rl的左子树挂接到T的右子树上，rl为新根
case RH:
R->bf=EH;
T->bf=LH;
break;
case LH:
R->bf=RH;
T->bf=EH;
break;
default:
break;
}
rl->bf=EH;
R_Rotate(T->rchild); //先左旋，以T->rchild为根左旋。
L_Rotate(T); //右旋，以T为根, 左旋后 T是和rl想等，rl是新根
break;
}
}
void LeftBalance(BiTree *T)
{
BiTree L,lr;
L=T->lchild;
switch (L->bf)
{
case EH:
L->bf=RH;
T->bf=LH;
R_Rotate(T);
break;
case LH:
L->bf=T->bf=EH;
R_Rotate(T);
break;
case RH:
lr=L->rchild;
switch (lr->bf)
{
case EH:
L->bf=L->bf=EH;
case RH:
T->bf=EH;
L->bf=LH;
break;
case LH:
L->bf=EH;
T->bf=RH;
break;
default:
break;
}
lr->bf=EH;
L_Rotate(T->lchild);
R_Rotate(T);
break;
default:
break;
}
}
bool InsertAVLtree(BiTree *T,int key,bool *taller)
{
if(!T) //此树为空
{
T=new BitNode; //直接作为整棵树的根。
T->bf=EH;
T->lchild=T->rchild=NULL;
T->data=key;
taller=true;
return true;
}
else
{
if(key==T->data) //已有元素，不用插入了，返回false；
{
taller=false;
return false;
}
if(key<T->data) //所插元素小于此根的值，就找他的左孩子去比
{
if(!InsertAVLtree(T->lchild,key,taller)) //所插元素小于此根的值，就找他的左孩子去比
{
return false;
}
if(taller) //taller为根，则树长高了，并且插入到了此根的左子树上。
{
switch (T->bf) //此根的平衡因子
{
case EH: //原先是左右平衡，等高
T->bf=LH; //由于插入到左子树上，导致左高=》》LH
taller=true; //继续往上递归
break;
case LH:
LeftBalance(T); //原先LH，由于插入到了左边，这T这个树，不平衡需要左平衡
taller=false; //以平衡，设taller为false，往上递归就不用进入此语句了，
break;
case RH:
T->bf=EH; //原先RH，由于插入到左边，导致此T平衡
taller=false;
break;
default:
break;
}
}
}
else
{
if(!InsertAVLtree(T->rchild,key,taller))
{
return false;
}
if(taller)
{
switch (T->bf)
{
case EH:
T->bf=RH;
taller=true;
break;
case LH:
T->bf=EH;
taller=false;
break;
case RH:
RightBalance(T);
taller=false;
break;
default:
break;
}
}
}
}
}
//中序遍历输出
void InOrderReverse(BiTree *T)
{
if(T)
{
InOrderReverse(T->lchild);
cout<<T->data<<endl;
InOrderReverse(T->rchild);
}
}
多路查找树
特点：每个节点可以有多个孩子，且可以存储多个元素，所有元素存在特定关系
2-3树
每个节点有2个或3个孩子。
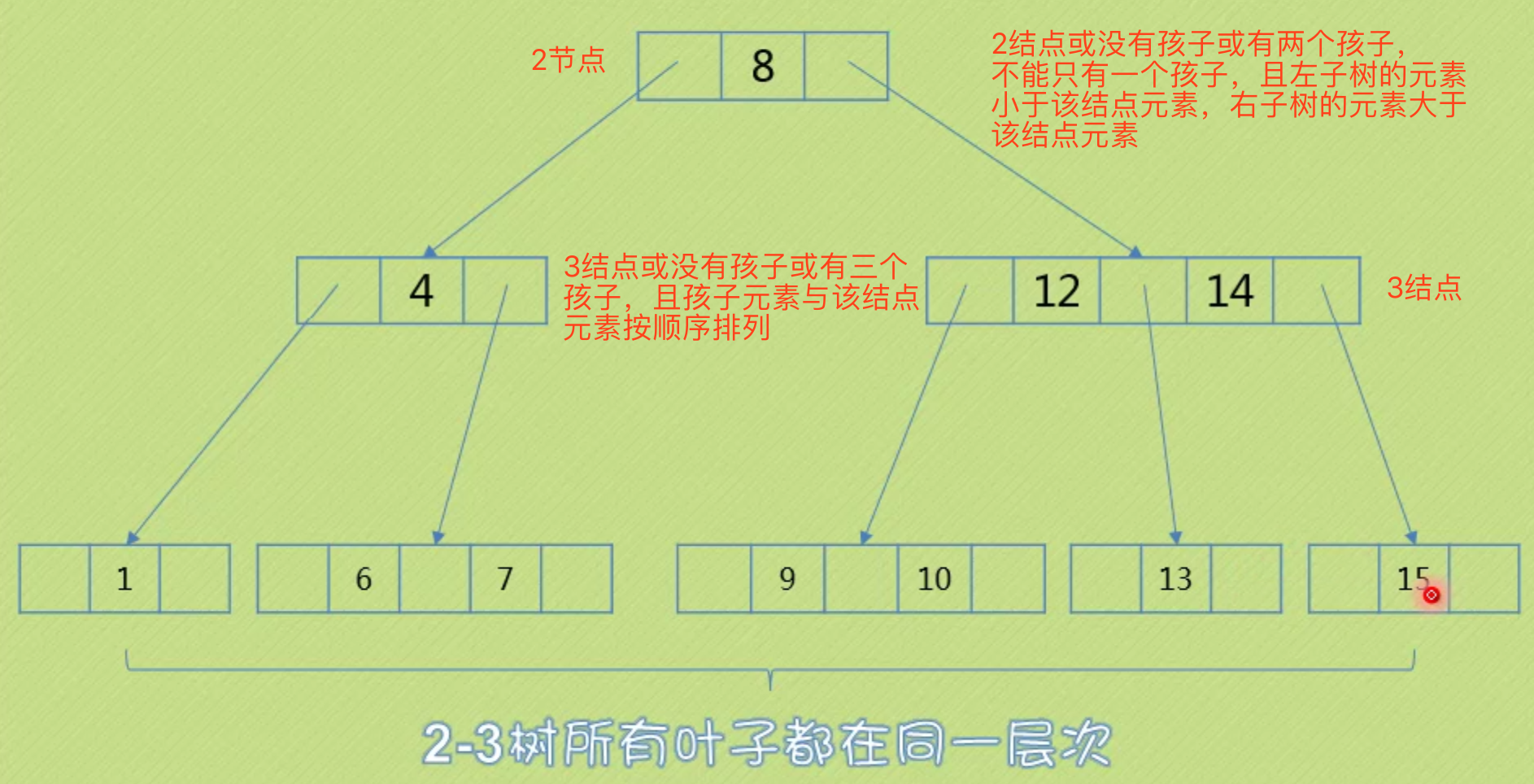
2-3-4树
同2-3树
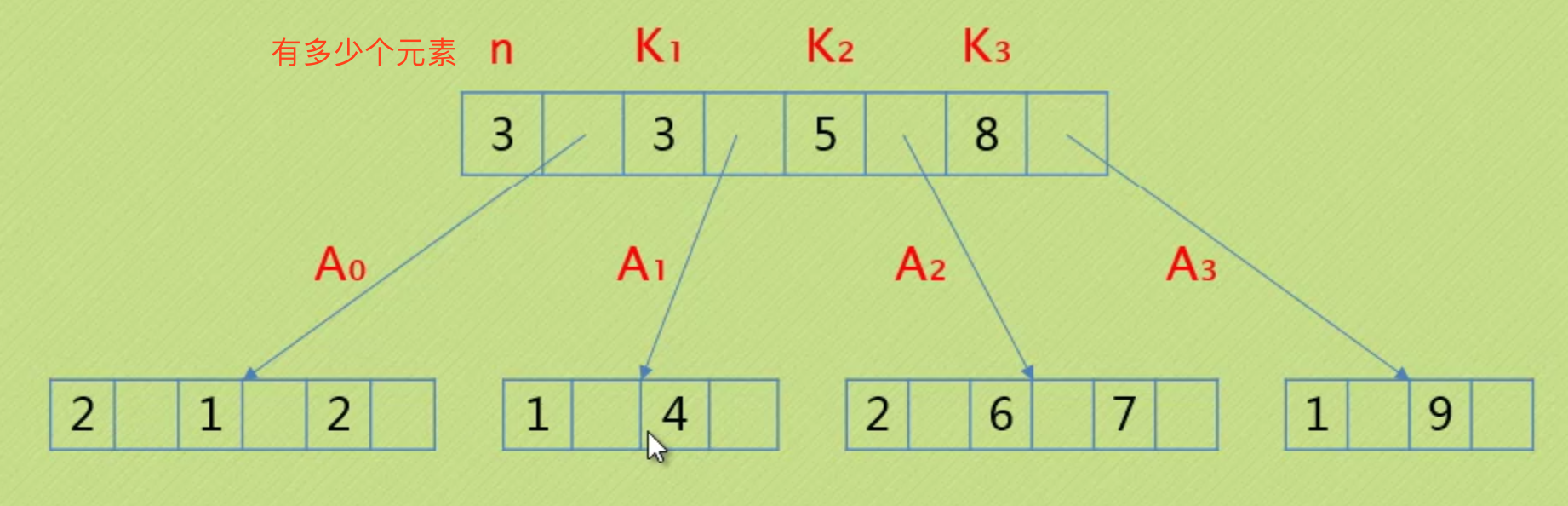
B树
一种平衡的多路查找树，2-3树和2-3-4树都是B树的特例。
我们把结点最大的孩子书的数目称为B树的阶，2-3树是3阶的B树，2-3-4树是4阶的B树。
散列表（哈希表）查找
在存储和查找的时候，通关关键字和散列函数计算出查找数据的位置，适用于一对一的映射关系数据。
构造散列函数
- 计算简单
- 分布均匀
直接定值法
采用某个线性函数值作为散列地址：f(key) = a * key + b
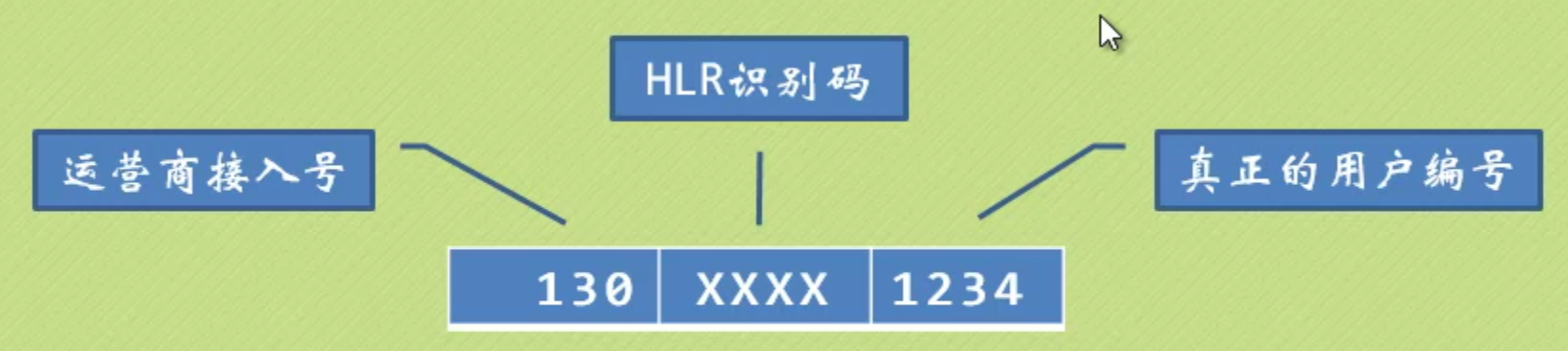
数字分析法
数字分析法通常适合处理关键字位数比较大的情况，比如手机号，我们可以抽取后四位作为散列地址。
平方取中法
将关键字平方之后去中间若干位数字作为三列地址，适用于不清楚关键字的分布，且关键字不大的情况。
折叠法
将关键字从左到右分割成位数相等的几部分，然后将这几部分叠加求和，并按散列表表长取后几位作为散列地址，适用于不清楚关键字分布，且关键字比较大的情况。
除留余数法
此方法为最常用的构造散列函数的方法，对于散列表长为m的散列函数计算公式为：f(key) = key mod p(p <= m)
随机数法
选择一个随机数，取关键字的随机函数值为他的散列地址，f(key) = random(key),适用于关键字不等的情况。
处理散列冲突
当key1 ！= key2，f(key1) = f(key2),则为冲突。
开放定址法
一旦发生冲突，就去寻找下一个空的散列地址，只要散列表足够大，空的散列地址总能找到，并将记录存入其中。
公式1：fi(key) = (f(key) + di) MOD m (di=1,2,…m-1)
例如：采用除留取余法过程中产生了冲突，我们就采用上边的方法，算出当前key值得散列地址。
可以修改di的值，例如使用平方运算来尽量解决堆积的问题。
公式2：fi(key) = (f(key) + di) MOD m (di=\(1^2\),-\(1^2\),\(2^2\),-\(2^2\),…\(q^2\),-\(q^2\),q<=m/2)
再散列函数法
采用多个散列函数
链地址法
将产生冲突的数据用链表的形式存储。
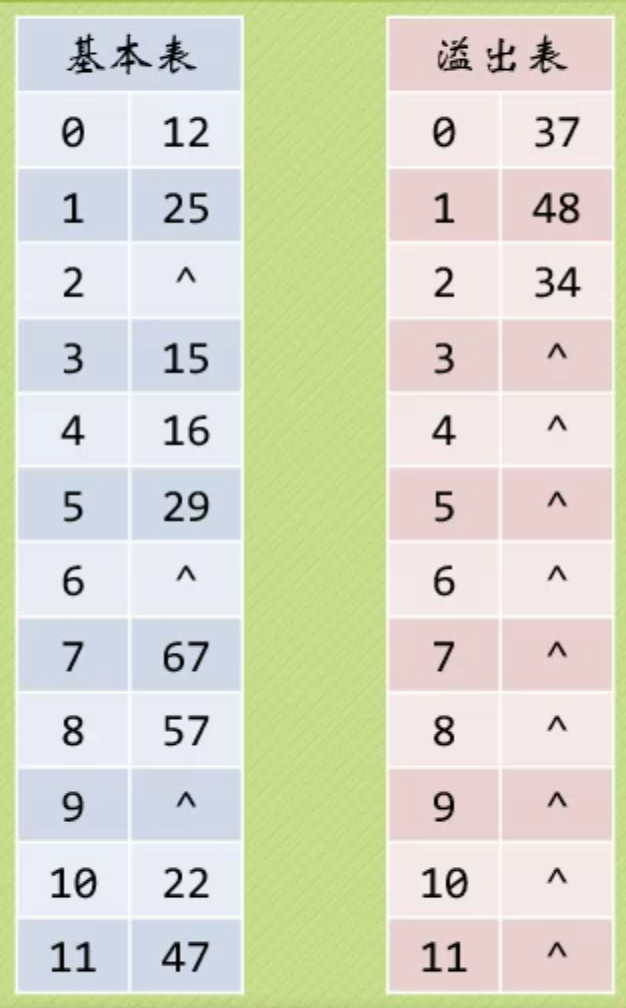
公共溢出区法
现在基本表进行查找，再到溢出表查找，凡是冲突的数据都会放到溢出表中。
